filmov
tv
Taylor series | Chapter 11, Essence of calculus
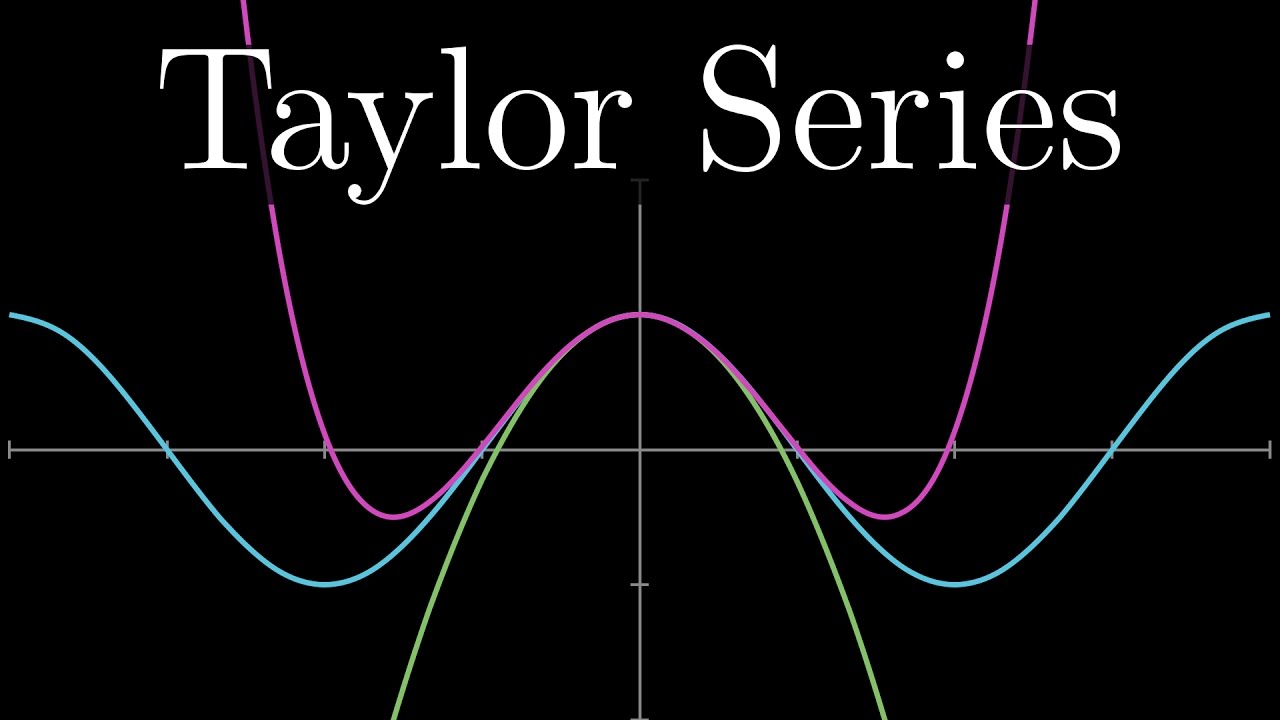
Показать описание
Taylor polynomials are incredibly powerful for approximations and analysis.
An equally valuable form of support is to simply share some of the videos.
Series like this one are funded largely by the community, through Patreon, where supporters get early access as the series is being produced.
Timestamps
0:00 - Approximating cos(x)
8:24 - Generalizing
13:34 - e^x
14:25 - Geometric meaning of the second term
17:13 - Convergence issues
Thanks to these viewers for their contributions to translations
Hebrew: Omer Tuchfeld
Vietnamese: ngvutuan2811
------------------
3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).
Various social media stuffs:
An equally valuable form of support is to simply share some of the videos.
Series like this one are funded largely by the community, through Patreon, where supporters get early access as the series is being produced.
Timestamps
0:00 - Approximating cos(x)
8:24 - Generalizing
13:34 - e^x
14:25 - Geometric meaning of the second term
17:13 - Convergence issues
Thanks to these viewers for their contributions to translations
Hebrew: Omer Tuchfeld
Vietnamese: ngvutuan2811
------------------
3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).
Various social media stuffs:
Taylor series | Chapter 11, Essence of calculus
Taylor Swift explains the Taylor series in 90 seconds
Taylor Series and Maclaurin Series - Calculus 2
Taylor and Maclaurin Series
Nemanja Nikitovic Live Stream (Calculus2 Ch 11 Taylor Series + Kalk of Power Series)
Cross products in the light of linear transformations | Chapter 11, Essence of linear algebra
MATH 2414 – 11.4 Working with Taylor Series
Lesson 11.4: Working with Taylor Series
btech m1 maths|multivariable calculus partial differen|verify the continues f(x, y) = 3xy/(x²+Y²)
Nemanja Nikitovic Live Stream (Calculus2 11.1 and 11.3 Power Series and Taylor Series)
MATH 2414 – 11.3 Taylor Series
Chapter 11 Section 10
Taylor Series - Calculus II
Lesson 11.3: Taylor Series
u CAN learn AP Calculus! Chapter 11-3 Taylor Series
(34min) u CAN kearn AP Calculus! Chapter 11-3 Taylor Series
This chapter closes now, for the next one to begin. 🥂✨.#iitbombay #convocation
Salsa Night in IIT Bombay #shorts #salsa #dance #iit #iitbombay #motivation #trending #viral #jee
Dear Calculus 2 Students, This is why you're learning Taylor Series
NEWYES Calculator VS Casio calculator
IIT Bombay CSE 😍 #shorts #iit #iitbombay
Chapter 11 Final Review
11 10 Taylor and Maclaurin Series 2
That's Why Mohit Sir Called 'God Of Mathematics'| Puzzle Brain teaser | #competishun ...
Комментарии
 0:22:20
0:22:20
 0:01:29
0:01:29
 0:29:22
0:29:22
 0:09:34
0:09:34
 1:02:06
1:02:06
 0:13:10
0:13:10
 0:39:23
0:39:23
 1:10:59
1:10:59
 0:13:31
0:13:31
 1:21:50
1:21:50
 0:59:54
0:59:54
 0:50:22
0:50:22
 0:45:26
0:45:26
 1:28:21
1:28:21
 0:10:54
0:10:54
 0:34:01
0:34:01
 0:00:16
0:00:16
 0:00:14
0:00:14
 0:12:36
0:12:36
 0:00:14
0:00:14
 0:00:11
0:00:11
 0:44:52
0:44:52
 0:21:57
0:21:57
 0:00:19
0:00:19