filmov
tv
Complex Analysis: Integral of xsin(x)/(x^2+1) using Contour Integration

Показать описание
Today, we use contour integration and the residue theorem to evaluate an improper integral.
Laplace Transform Method:
Laplace Transform Method:
Complex Analysis: Integral of xsin(x)/(x^2+1) using Contour Integration
Let's do complex analysis: Integrating sin^2(x)/x^2(x^2+1) from 0 to infinity using residue the...
Complex Analysis: Integral of sin(x)/x using Contour Integration
Integral xsinx/1+x^2 from 0 to infinity
Integral of 1/(x^2+1) from -inf to inf, Contour Integral
Residue Theorem (Definite Integrals) || Complex Analysis || MAT324
By Using Contour Integration Type 02 Problems 01 -Complex Integration
Complex Analysis: Integral of 1/(x^4-x^2+1) using Contour Integration
Complex Analysis: Integral of (x-sin(x))/x^3
Complex Analysis: Integral of (1-cos(x))/x^2 using Contour Integration
Integral of sinx/x complex analysis close contour residus theorem
Contour integration ( When poles lies on tha real axis)(Complex Analysis)
Complex analysis integral of sin(x^2) fresnel integrals
By Using Contour Integration Type 03 Problems -Complex Integration
Byproduct and Bonus integral, x sin(a x)/(x^2+b^2) and sin(a x)/(x(x^2+b^2)) from 0 to infinity
Contour Integral, General Case cos(ax)/(x^2+b^2), from 0 to infinity
2 ridiculously awesome log integrals solved using contour integration
Application of Cauchy Residue Theorem | Contour Integration | Contour Integral Complex Analysis
By Using Contour Integration Type 01 Problems 02 -Complex Integration
Contour Integration. Type :2 ( Algebric Functions in Improper Integrals) in Complex Analysis.
Lecture 2|Improper Integrals by Contour Integration|Theorem and examples|Theta Classes
Applying contour integration to real integrals -- Complex Analysis 23
This chapter closes now, for the next one to begin. 🥂✨.#iitbombay #convocation
Complex Analysis: A Trigonometric Integral
Комментарии
 0:17:37
0:17:37
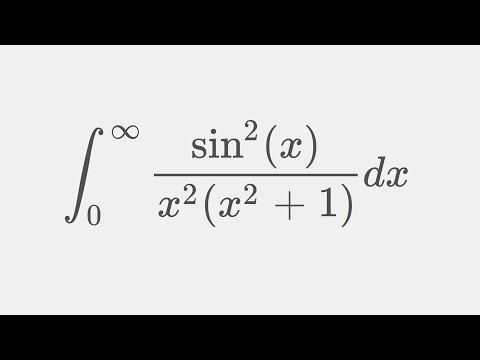 0:28:16
0:28:16
 0:17:43
0:17:43
 0:08:45
0:08:45
 0:19:50
0:19:50
 0:25:06
0:25:06
 0:17:13
0:17:13
 0:18:31
0:18:31
 0:14:26
0:14:26
 0:34:20
0:34:20
 0:18:14
0:18:14
 0:14:24
0:14:24
 0:07:48
0:07:48
 0:12:23
0:12:23
 0:03:33
0:03:33
 0:03:23
0:03:23
 0:26:14
0:26:14
 0:44:43
0:44:43
 0:14:49
0:14:49
 0:23:42
0:23:42
 0:54:24
0:54:24
 0:39:10
0:39:10
 0:00:16
0:00:16
 0:16:46
0:16:46