filmov
tv
Find the Angle in this Cyclic Quadrilateral | Fast & Easy Tutorial
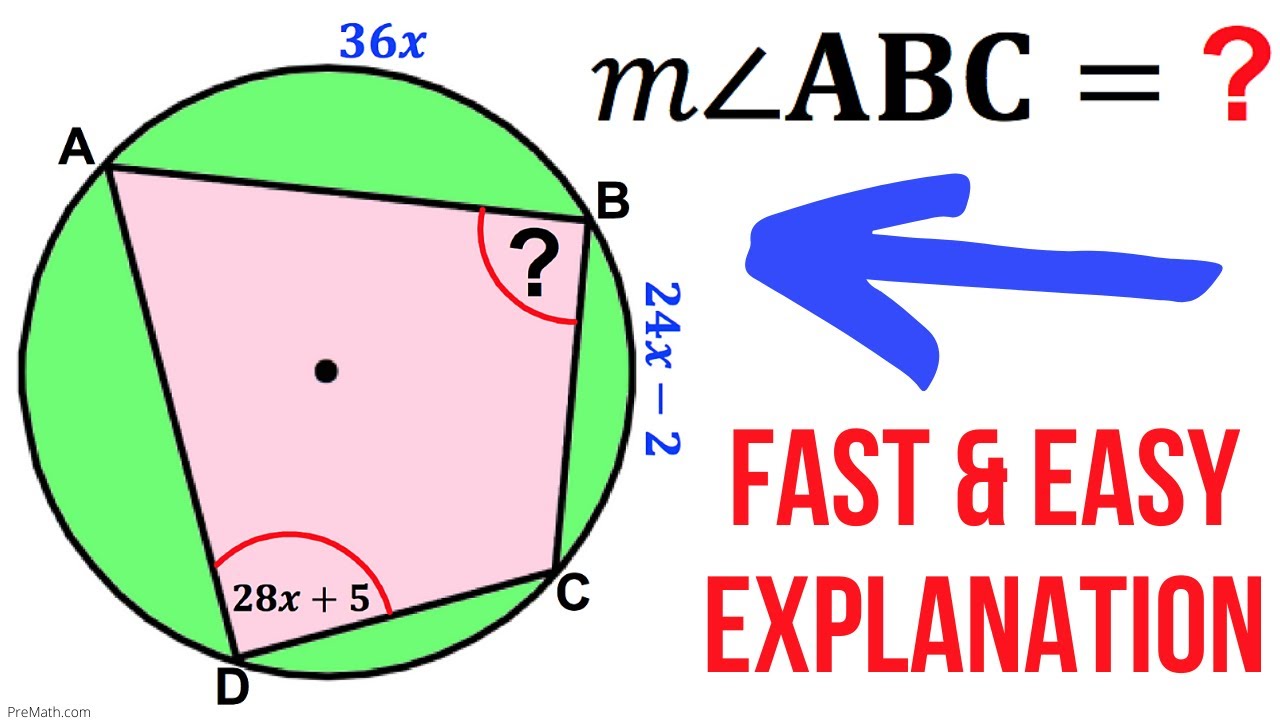
Показать описание
How do you find the angle? Let’s see…
Can You Find Angle X? | Geometry Challenge!
Missing Angles in Triangles | How to Find the Missing Angle of a Triangle Step by Step
Challenge Question: Can you find the Angle X?| Step-by-Step Explanation
How To Calculate The Missing Angle In a Triangle
Can you find the Angle X? | Quick & Simple Tutorial
how to find the degree of an angle using a speed square
Angles of Triangle: Sum of Interior Angles and Exterior Angle Theorem by @MathTeacherGon
Finding the Missing Angle of a Triangle: A Step-by-Step Guide | Triangles | Math with Mr. J
Math Antics - Angle Basics
GCSE Maths - Alternate, Corresponding and Allied Angles - Parallel Lines Angle Rules #117
How To Find The Reference Angle In Radians and Degrees - Trigonometry
How to find the angle of a rafter with a speed square ( check the description for the whole process)
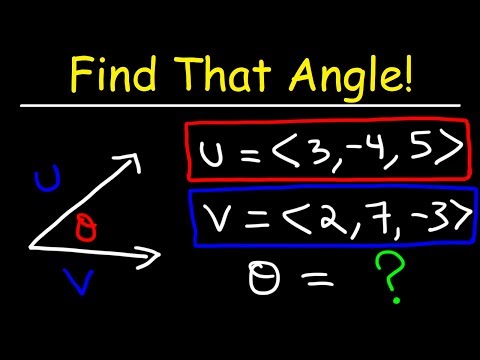
How to find the Angle between Vectors
Finding The Angle Between Two Vectors - Calculus 3
Geometry - Ch. 1: Basic Concepts (20 of 49) Find the Angle Measures=?: Example 1
GCSE Maths - 5 Angle Rules to Know #116
How To Find An Angle Using A Speed Square #shorts #tools
Using a Speed Square as an Angle Finder #carpentry #tips #tricks #angles #speedsquare
PARALLEL LINES AND TRANSVERSALS | Find the Angle Measure | Geometry Online Lesson
Using Angle Relationships to Find Unknown Angles
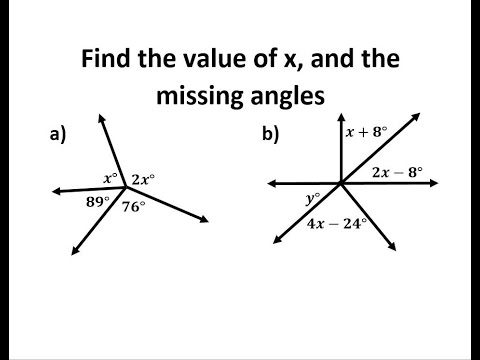
Find the Value of x, and the Missing Angle Measures
Exterior Angle Theorem For Triangles, Practice Problems - Geometry
Find any rafter angle with only a Speed Square and Chalk Line!!
Комментарии
 0:15:46
0:15:46
 0:08:44
0:08:44
 0:03:40
0:03:40
 0:08:05
0:08:05
 0:14:33
0:14:33
 0:04:44
0:04:44
 0:01:13
0:01:13
 0:07:00
0:07:00
 0:05:14
0:05:14
 0:07:46
0:07:46
 0:05:36
0:05:36
 0:12:28
0:12:28
 0:03:22
0:03:22
 0:05:44
0:05:44
 0:10:07
0:10:07
 0:03:48
0:03:48
 0:08:27
0:08:27
 0:00:25
0:00:25
 0:00:59
0:00:59
 0:06:44
0:06:44
 0:14:30
0:14:30
 0:10:07
0:10:07
 0:12:41
0:12:41
 0:01:27
0:01:27