filmov
tv
Math 391 Lecture 17 - Conclusion of higher order equations and Series Solutions to linear ODEs
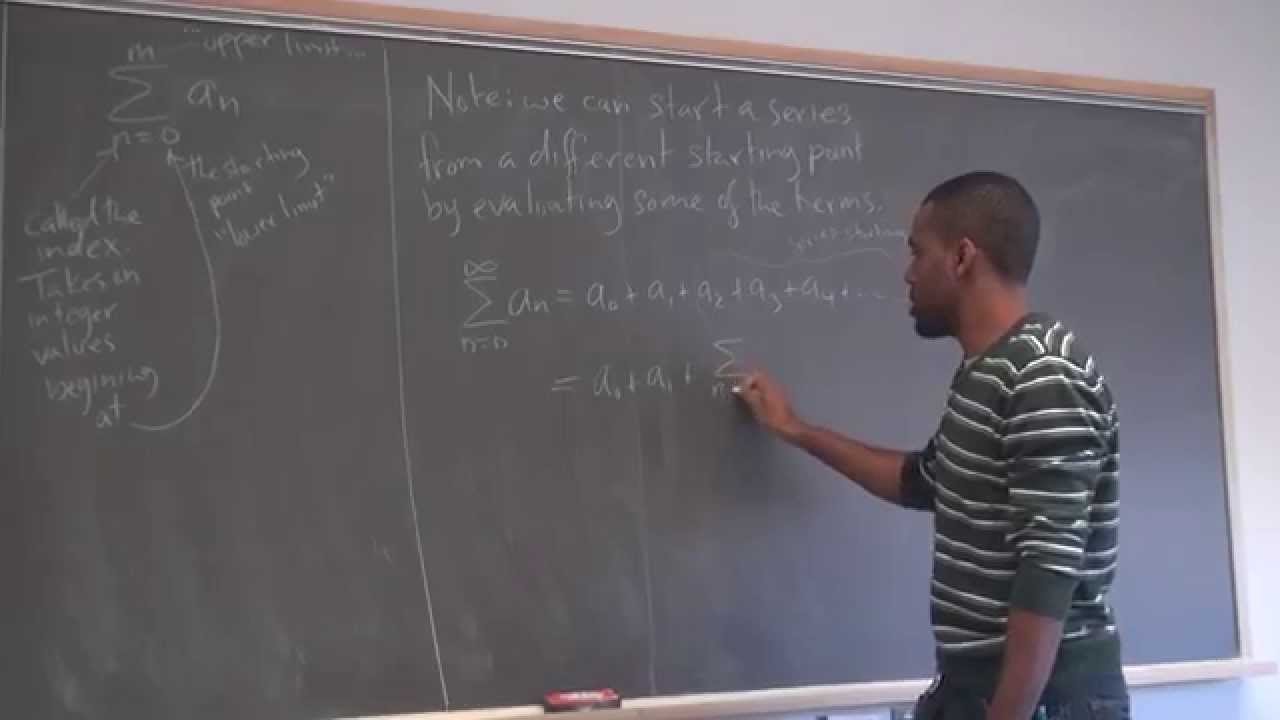
Показать описание
We had technical difficulties today :( apparently, the first 5 to 10 minutes of the lecture wasn't recorded. I believe all the worked out examples I did were caught for a short time on camera though.
Anyway, in this lecture we looked over a couple more techniques for solving higher order differential equations (third order or higher), and then moved on to series solutions for second order linear equations (SOLDEs).
We went over some basic concepts and properties of series for most of the remaining lecture. As we had some time left over, I rushed through an example of solving a simple SOLDE via series.
The idea: assume the solution to an ODE takes on the form of a power series. Find the necessary derivatives through term-by-term differentiation, plug into the ODE and obtain a recurrence relation for determining the coefficients of your power series. There are some subtle techniques needed to pull this off, and our short review of series gave us the tools and know how to do this. More examples to come in the next lecture.
Anyway, in this lecture we looked over a couple more techniques for solving higher order differential equations (third order or higher), and then moved on to series solutions for second order linear equations (SOLDEs).
We went over some basic concepts and properties of series for most of the remaining lecture. As we had some time left over, I rushed through an example of solving a simple SOLDE via series.
The idea: assume the solution to an ODE takes on the form of a power series. Find the necessary derivatives through term-by-term differentiation, plug into the ODE and obtain a recurrence relation for determining the coefficients of your power series. There are some subtle techniques needed to pull this off, and our short review of series gave us the tools and know how to do this. More examples to come in the next lecture.
1:00:17
Math 391 Lecture 17 - Conclusion of higher order equations and Series Solutions to linear ODEs
1:40:34
Math 391 1XC Lecture 17 - Euler Equations and Series Solutions near Regular Singular Points
1:48:54
Math 391 1XC Lecture 18 - The Laplace Transform and using it to solve linear ODEs
1:39:22
Math 391 1XC Lecture 7 - Misc ODEs;The Bernoulli First Order ODE, Complex Numbers; Euler's Iden...
1:04:18
Math 391 Lecture 18 - Series Solutions to second order linear differential equations contd
0:07:14
This is always divisible by 391??
1:52:46
Math 391 1XC Lecture 20 - Sturm-Liouville Theory; The Eigenvalue Problem; and The Heat Equation
0:55:39
Math 391 Lecture 21 - Finding Laplace Transforms and using them to solve ODEs
1:51:41
Math 391 1XC Lecture 21 - Final Exam Review
3:01:13
Math 1206-L11 Lecture 17 - Applications of Integrals; Integration by Parts; Tabular Integration
0:00:13
Indian vs Japanese Maths 🔥| Vedic Maths Trick for Fast Calculation | Speed Maths #trending #shorts...
1:02:19
Math 391 Lecture 19 - More series solutions, Euler Equations and Singular Points
1:09:44
Math 391 Lecture 16 - Higher Order Linear Differential Equations
0:00:24
Genius IQ Test-Maths Puzzles | Tricky Riddles | Maths Game | Paheliyan with Answers | Tricky Paheli
1:44:07
Math 391 1XC Lecture 14 - EUT for first order nonlinear ODEs; Intervals of solutions; Series Review
1:07:50
Math 391 Lecture 6 - Exact Equations and Reduction of Order
0:39:17
Math 391 Lecture 15 - Short review of chapter 3 - Test 2 preparation
1:07:18
Math 392 Lecture 18 - End of Divergence Theorem, summary of Calculus, Beginning of Linear Algebra!
0:56:27
Math 391 Lecture 9 - SOLDEs with constant coefficients and the Existence and Uniqueness Theorem
0:00:52
Fast Percentage Trick
0:00:21
Ek jhatke mein ho jayega The End 💔
1:37:24
Math 391 1XC Lecture 16 - More on Series Solutions; and Euler Equations
0:52:39
Math 391 Lecture 5 - Modeling with linear equations continued - Mixture Problems
0:59:58
Math 391 Lecture 14 - Mechanical Vibrations - Motion of a mass at the end of a vibrating spring
Комментарии