filmov
tv
Math 391 Lecture 6 - Exact Equations and Reduction of Order
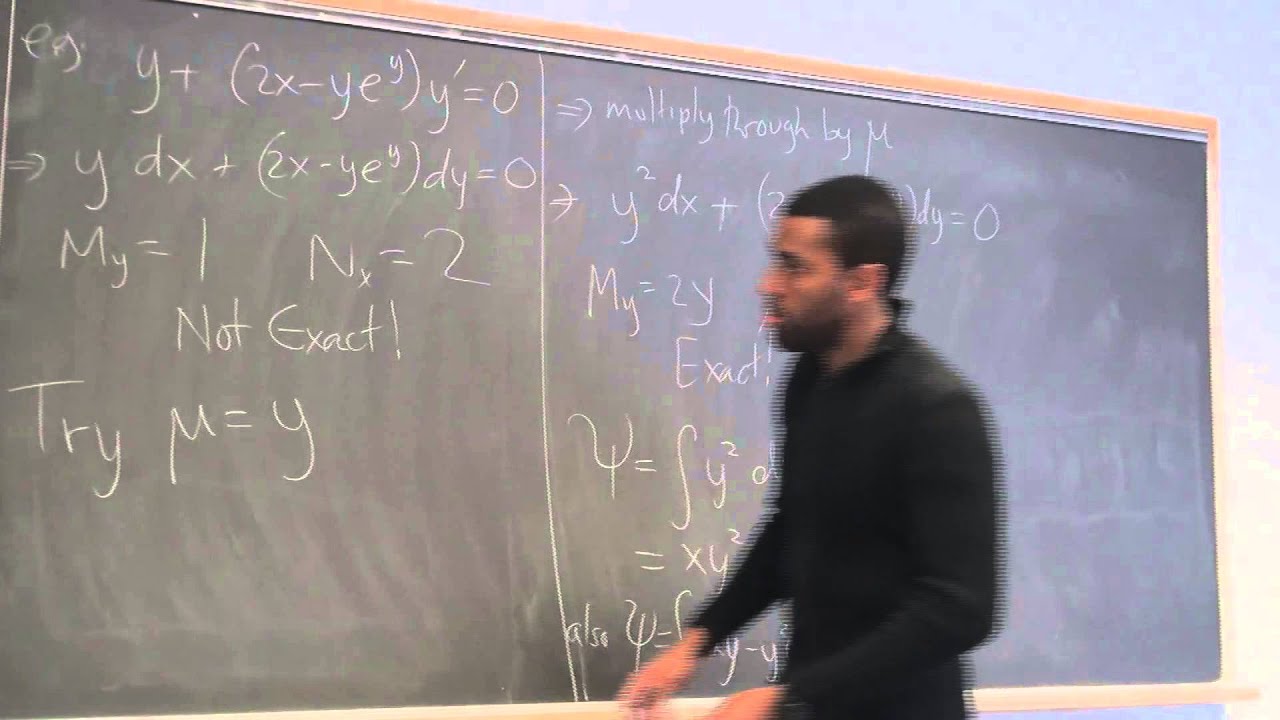
Показать описание
In this lecture, we complete the topics required for the first test--Section 2.6 Exact Equations, and the miscellaneous section of 2.9 where we look at the Reduction of Order technique (we will look at even more techniques next time). We define what an exact differential equation is, how to tell when an equation is exact and how to find the solution to an ODE given that it is exact. We cover two methods of finding a solution to an exact equation, and do a few examples.
We end by doing one example of a reduction of order problem--where we used a substitution to change a second order ODE into a first order ODE, and hence solved it. We stop at only one example, since in this context the technique is straight forward, and we shall revisit reduction of order in a later chapter, in a more general context.
We end by doing one example of a reduction of order problem--where we used a substitution to change a second order ODE into a first order ODE, and hence solved it. We stop at only one example, since in this context the technique is straight forward, and we shall revisit reduction of order in a later chapter, in a more general context.
Math 391 Lecture 6 - Exact Equations and Reduction of Order
Math 391 1XC Lecture 6 - Exact Equations with Integrating Factors
Math 391 1XC Lecture 5 - Continuous Compounding; Newton's Cooling Law; Exact Differential Equat...
Math 391 1XC Lecture 7 - Misc ODEs;The Bernoulli First Order ODE, Complex Numbers; Euler's Iden...
Math 391 Lecture 4 - Homogeneous 1st order ODEs and modeling with first order linear ODEs
Math 391 Lecture 5 - Modeling with linear equations continued - Mixture Problems
Math 391 Lecture 18 - Series Solutions to second order linear differential equations contd
Math 391 Lecture 8 - Some miscellaneous first order ODEs and Intro to Second order linear ODEs
Math 391 1XC Lecture 4 - Modeling with First Order ODEs: Mixture Problems and Continuous Compounding
Math 391 Lecture 11 - Complex roots - Repeated roots - Reduction of order
Math 391 1XC Lecture 18 - The Laplace Transform and using it to solve linear ODEs
Differential Equations, Lecture #6, Slope Fields, Existence & Uniqueness, Phase Lines
Math 391 1XC Lecture 21 - Final Exam Review
Math 391 Lecture 2 - Intro to differential equations - definitions and separation of variables
Math 391 1XC Lecture 2 - Population Models and First Order Linear Differential Equations
Math 391 Lecture 17 - Conclusion of higher order equations and Series Solutions to linear ODEs
Math 391 Lecture 23 - Separation of Variables for PDEs and the Heat Equation
Math 391 Lecture 7 - Chapter 2 HW review - part 1
Math 391 Lecture 21 - Finding Laplace Transforms and using them to solve ODEs
Math 391 Lecture 15 - Short review of chapter 3 - Test 2 preparation
Math 391 Lecture 1 - Intro and a very brief (and incomplete) overview of ODEs
Lecture 6 || LUB GLB || Real Analysis || Anindya S. Das (JAM AIR 391) on @DrMathAcademy
Nick Sibicky Go Lecture #391 - Sloppy 6-Dan Game
Math 391 Lecture 7 - Chapter 2 HW review - part 2
Комментарии
 1:07:50
1:07:50
 1:12:15
1:12:15
 1:38:26
1:38:26
 1:39:22
1:39:22
 0:58:20
0:58:20
 0:52:39
0:52:39
 1:04:18
1:04:18
 0:32:38
0:32:38
 1:37:14
1:37:14
 0:46:47
0:46:47
 1:48:54
1:48:54
 0:49:40
0:49:40
 1:51:41
1:51:41
 0:48:22
0:48:22
 1:37:23
1:37:23
 1:00:17
1:00:17
 1:01:53
1:01:53
 0:40:47
0:40:47
 0:55:39
0:55:39
 0:39:17
0:39:17
 0:48:45
0:48:45
 0:30:00
0:30:00
 0:49:44
0:49:44
 0:03:26
0:03:26