filmov
tv
Example of L'Hopital's Rule (Hard)

Показать описание
Calculus: We compute the limit of (1-cos(x))^3/2 /sin(x) as x goes to zero. A straightforward approach with multiple applications of L'Hopital's rule fails. We consider options, based on trig identities and square roots.
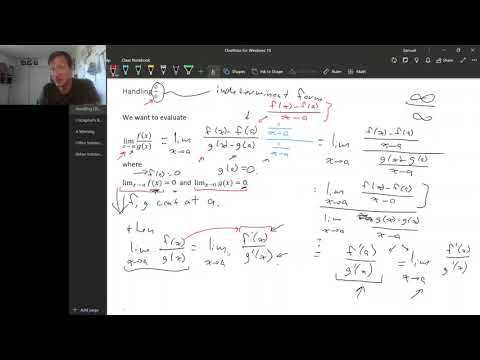
L'hopital's rule
Example of L'Hopital's Rule (Hard)
L'Hopital's Rule - Hard Example
L'Hospital's Rule, Derivative, Limits, Example - Calculus
42: L'Hôpital's Rule - example (oo/oo trig)
Understanding Limits and L'Hospital's Rule
L'Hopital's Rule - Hard Example 2
L'Hopital's Rule ultimate study guide
Tricky L'Hopital's Rule problem | Derivative applications | Differential Calculus | Khan A...
'Proof' of L'Hospital's Rule
4.8 1 - Hard Limits - L'Hospital's Rule
L'Hopitals Rule Exam Practice Problems
Hard L'Hospital's rule example
L'Hopital's Rule - Finding a, b using L'Hopital's Rule | A Tricky Question | Cal...
L'Hopital's Rule | Indeterminate form Infinity minus Infinity | A Hard Example | Calculus
42: L'Hôpital's Rule - example (oo/oo poly)
virtuallymath.com: example of L'Hopital's rule from calculus
Calculus 6.08b - L'Hopital's Rule
Calculus 1: L'Hospital's Rule (14 of 25) Example 13
L'Hopital's Rule Example.mp4
L'Hopital's Rule Part 1
Finding Limits Using L' Hopital's Rule (Exponents & Square Roots)
Limits requiring L'Hopital's Rule
42: L'Hôpital's Rule - example (0/0, trig)
Комментарии
 0:13:09
0:13:09
 0:05:35
0:05:35
 0:06:49
0:06:49
 0:00:37
0:00:37
 0:02:35
0:02:35
 0:09:12
0:09:12
 0:04:22
0:04:22
 0:44:56
0:44:56
 0:13:10
0:13:10
 0:10:44
0:10:44
 0:16:09
0:16:09
 0:07:06
0:07:06
 0:09:26
0:09:26
 0:08:30
0:08:30
 0:11:06
0:11:06
 0:02:54
0:02:54
 0:08:22
0:08:22
 0:08:41
0:08:41
 0:06:29
0:06:29
 0:07:40
0:07:40
 0:08:26
0:08:26
 0:03:11
0:03:11
 0:16:35
0:16:35
 0:03:23
0:03:23