filmov
tv
Understanding Limits and L'Hospital's Rule

Показать описание
We learned about limits earlier in this series. We know what they represent, and we know how to evaluate them. Then we found that we don't need them that much, because we have better methods for differentiating functions than all that business with tangent lines and limits. But limits still have applications, and we can use them to find out the value of a function at a certain point when we can't figure this out from the function itself. How? With L'Hospital's rule!
Check out "Is This Wi-Fi Organic?", my book on disarming pseudoscience!
Check out "Is This Wi-Fi Organic?", my book on disarming pseudoscience!
Understanding Limits and L'Hospital's Rule
L'hopital's rule
US presidents explain L'Hôpital's rule in under 90 seconds
Limits, L'Hôpital's rule, and epsilon delta definitions | Chapter 7, Essence of calculus
Introduction to l'Hôpital's rule | Derivative applications | Differential Calculus | Khan ...
Did L'Hospital Steal his Rule?
L'Hospital's Rule, Derivative, Limits, Example - Calculus
This is a very famous limit
L'hospitals Rule in 57 Seconds!! (Calculus)
How to apply L'Hopital's Rule to evaluate the limit
easiest method to. solve limit by L Hospital rule #maths #limit #subscribe
L'Hôpital's rule | JMDI DEFENCE ACADEMY | NDA 2023 | NDA foundation
L' Hospital Rule | Limits | #jeedailyconcepts
L'Hopital's Rule ultimate study guide
The limit is the limit is the limit is the limit
How to use L'Hopital's Rule to Find the Limit of ln(ln(x))/x as x approaches Infinity #sho...
You will love this Rule!! #calculus
L'Hospital's Rule | Indeterminate Form Type 0/0 | y=tan(3x)/sin(2x)
Limits requiring L'Hopital's Rule
L’Hopitals Rule
Indeterminate Form
L Hospital rule for limit class 12 #shorts
L hospital rule|how to find limit#shorts
Visualize L’Hospital’s rule for the case of f(a)=g(a)=0. #calculus #limit
Комментарии
 0:09:12
0:09:12
 0:13:09
0:13:09
 0:01:25
0:01:25
 0:18:27
0:18:27
 0:08:52
0:08:52
 0:00:59
0:00:59
 0:00:37
0:00:37
 0:00:48
0:00:48
 0:00:57
0:00:57
 0:01:37
0:01:37
 0:00:49
0:00:49
 0:00:49
0:00:49
 0:00:56
0:00:56
 0:44:56
0:44:56
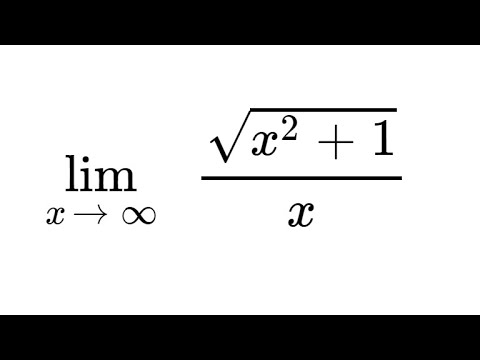 0:00:14
0:00:14
 0:00:43
0:00:43
 0:00:29
0:00:29
 0:01:00
0:01:00
 0:16:35
0:16:35
 0:00:32
0:00:32
 0:00:18
0:00:18
 0:00:05
0:00:05
 0:00:28
0:00:28
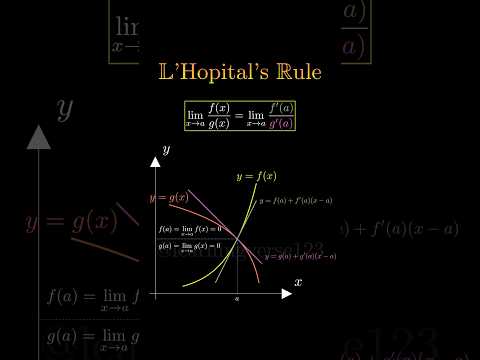 0:00:31
0:00:31