filmov
tv
Limits requiring L'Hopital's Rule
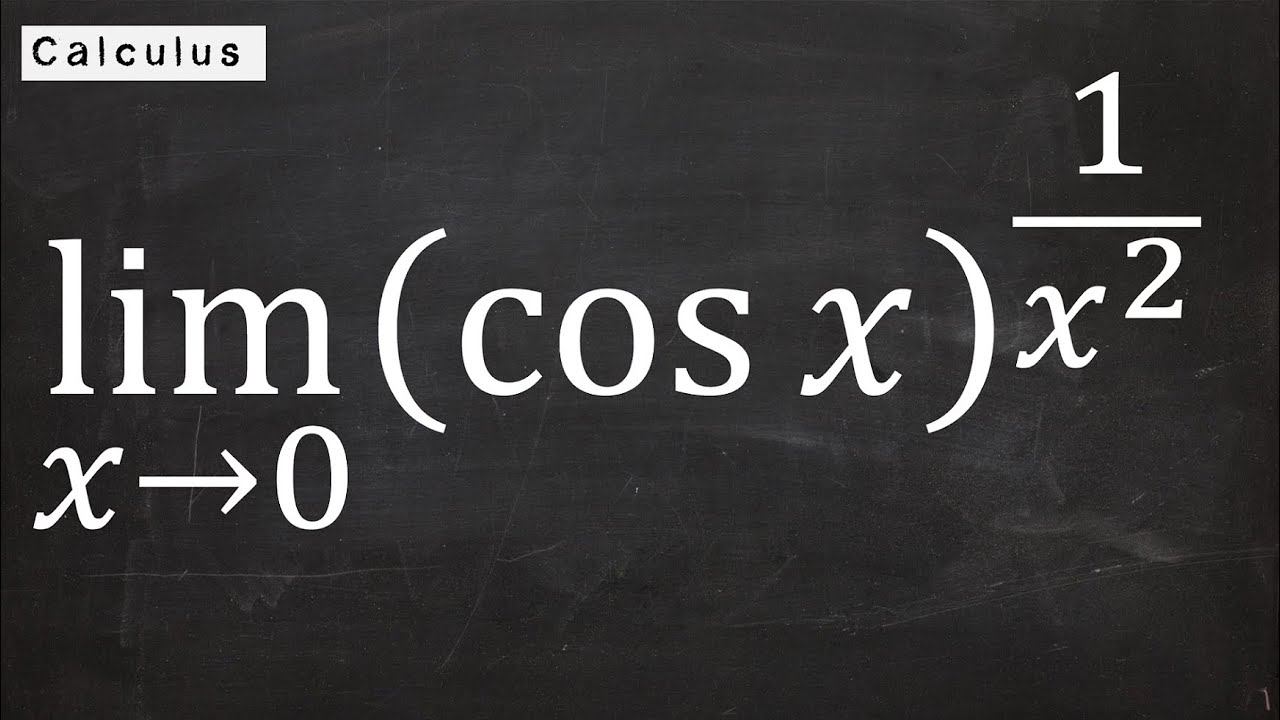
Показать описание
In this video showed how and when to use L'Hopital's rule ffor taking limits
L'hopital's rule
Limits requiring L'Hopital's Rule
When Not to Apply L'Hospital's Rule for Calculus Limits
L’Hospital’s Rule (2 Minutes)
L'Hospital's Rule, Derivative, Limits, Example - Calculus
L'Hopital's Rule ultimate study guide
'Proof' of L'Hospital's Rule
Calculus 1: L'Hospital's Rule (7 of 25) Example 6
Limit Practice Example (L’Hospital’s Rule)
PreCalculus | Limit of a function (l’hopital’s Rule)
L'Hospital's Rule Fails in This Limit Evaluation?
L'Hospital's Rule (5 basic examples)
L'Hospital's Rule - Limits Examples
L'Hopitals Rule For Continuous Compounding Formula Limits
IMPORTANT Limits L'Hopital's Rule IIT JEE IB AB AP Calculus Indeterminate Powers
Indeterminate Forms
Indeterminate Powers with Rational Exponent L Hopital's Rule for Limits
Find Mistake in Application of L'Hospital's Rule to Find Limit
Limit of an indeterminate form using L'Hopital's rule
L'Hopital's Rule Ex. 5 (Indeterminate Powers)
Using L'Hospital's Rule with Indeterminate form Infinity^0
📚 How to use L’Hospital’s Rule to find the limit of a function (Part 1)
Indeterminate Powers of Trigonometric Function L'Hopital's Rule Calculus
Evaluating the required limit using L' Hopital's rule and Taylor series expansion
Комментарии
 0:13:09
0:13:09
 0:16:35
0:16:35
 0:04:53
0:04:53
 0:02:13
0:02:13
 0:00:37
0:00:37
 0:44:56
0:44:56
 0:10:44
0:10:44
 0:02:12
0:02:12
 0:02:49
0:02:49
 0:07:26
0:07:26
 0:04:24
0:04:24
 0:12:57
0:12:57
 0:13:54
0:13:54
 0:08:34
0:08:34
 0:28:55
0:28:55
 0:07:31
0:07:31
 0:09:58
0:09:58
 0:04:27
0:04:27
 0:06:16
0:06:16
 0:11:41
0:11:41
 0:06:52
0:06:52
 0:04:54
0:04:54
 0:08:22
0:08:22
 0:03:44
0:03:44