filmov
tv
Solving Exponential Equations with Logarithms (Precalculus - College Algebra 64)

Показать описание
How to use logarithms to solve general exponential equations. Other techniques are also discussed.
How to Solve Exponential Equations using Logarithms - No Common Base Present
Solving exponential equation with logarithm | Logarithms | Algebra II | Khan Academy
Solving Exponential and Logarithmic Equations
Solving Exponential Equations with Logarithms (Precalculus - College Algebra 64)
Solving Exponential Equations
Ex 1: Solve Exponential Equations Using Logarithms
Solving exponential equations in terms of logs
Solving exponential equation | Exponential and logarithmic functions | Algebra II | Khan Academy
Solving Exponential Equations Using Logarithms/How to find the value of X
Solving Logarithmic Equations
Exponential Equation - Let’s solve the equation using logarithms
Learn how to take log of both sides to solve an exponential equation
Solving logarithmic equations | Exponential and logarithmic functions | Algebra II | Khan Academy
How to Solve Exponential Equations using Logarithms: Step-by-Step Technique
Introduction to Solving Logarithms and Exponentials (Precalculus - College Algebra 57)
Solving exponential equations by using the natural log
Kuta Tutorial: solving exponential equations with logarithms
Solving Exponential and Logarithmic Equations (Multiple Examples)
Solving Exponential Equation
How do I find x? Exponential equation with two different bases. Reddit precalculus r/Homworkhelp
Exponential Equations without Logarithms
Solve Exponential Equation Using Natural Logarithms
Ex: Write Exponential Equations as Logarithmic Equations - Variables
Ex 5: Solve Exponential Equations with Two Exponential Parts Using Logarithms
Комментарии
 0:05:47
0:05:47
 0:02:51
0:02:51
 0:07:08
0:07:08
 1:03:24
1:03:24
 0:16:36
0:16:36
 0:05:02
0:05:02
 0:10:07
0:10:07
 0:05:12
0:05:12
 0:07:16
0:07:16
 0:25:27
0:25:27
 0:14:37
0:14:37
 0:02:57
0:02:57
 0:04:13
0:04:13
 0:05:46
0:05:46
 0:34:46
0:34:46
 0:02:23
0:02:23
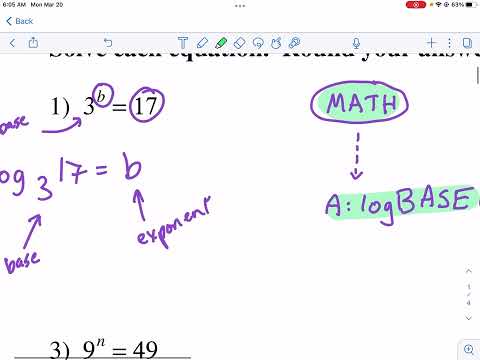 0:18:22
0:18:22
 0:12:27
0:12:27
 0:00:56
0:00:56
 0:07:47
0:07:47
 0:01:39
0:01:39
 0:04:24
0:04:24
 0:03:03
0:03:03
 0:05:41
0:05:41