filmov
tv
Prove: Volume of a Sphere (Disk Method)

Показать описание
Let's prove the formula for the volume of a sphere using disk method! Each step is carefully explained with an intuitive appeal--if you are looking for a comprehensive overview of the proof, this is the video for you!
Your support is truly a huge encouragement.
Please take a second to subscribe in order to send us your valuable support and receive notifications for new videos!
Every subscriber and like are immensely appreciated.
Your support is truly a huge encouragement.
Please take a second to subscribe in order to send us your valuable support and receive notifications for new videos!
Every subscriber and like are immensely appreciated.
Visualizing the Volume of a Sphere Formula | Deriving the Algebraic Formula With Animations
The Volume of a Sphere - Numberphile
Volume of a Sphere
Why is the volume of a sphere V=4/3*pi*r^3? (calculus disk method)
But why is a sphere's surface area four times its shadow?
Volume of a Sphere: Three Different Derivations
Volume of a Sphere
Archimedes derives the volume of a sphere #shorts
'Examining and Rectifying the Error in Heisenberg's Uncertainty Principle'
Proving the volume and the surface area of a sphere by using integrals
Cylinder, Cone, and Sphere Volume
Deriving the Equation of the Volume of a Sphere Using Triple Integration
Volume of a Sphere Formula PROVED (with calculus)
Volume of a Sphere (equation derived with calculus)
Volume of a Sphere | MathHelp.com
Volume of a Sphere, Disc Method, Prove It, Integration, Example - Calculus
Proof of the volume formula of a sphere (prove the volume of a sphere is v=(4/3)pi r^3)
Volume of sphere visual proof
Prove: Volume of a Sphere (Disk Method)
Volume of a Sphere -- Archimedes Calculation
Deriving the Volume of a Sphere
Derive the Volume of a Sphere using Integration
Why is the volume of a cone 1/3*pi*r^2*h? Here's a proof with the disc method! Calculus basics
Volume of a sphere with a triple integral
Комментарии
 0:03:12
0:03:12
 0:04:14
0:04:14
 0:04:55
0:04:55
 0:05:58
0:05:58
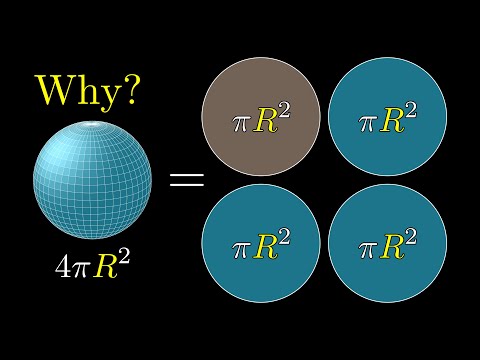 0:15:51
0:15:51
 0:04:46
0:04:46
 0:01:27
0:01:27
 0:01:00
0:01:00
 0:59:58
0:59:58
 0:13:41
0:13:41
 0:02:32
0:02:32
 0:00:51
0:00:51
 0:12:13
0:12:13
 0:02:28
0:02:28
 0:01:57
0:01:57
 0:00:42
0:00:42
 0:19:33
0:19:33
 0:01:29
0:01:29
 0:10:00
0:10:00
 0:00:43
0:00:43
 0:12:29
0:12:29
 0:14:34
0:14:34
 0:07:10
0:07:10
 0:07:21
0:07:21