filmov
tv
Deriving the Equation of the Volume of a Sphere Using Triple Integration

Показать описание
In this video, we go through the process of deriving the equation for the volume of a sphere using triple integration. We will start with basic calculus concepts and work our way up to advanced mathematical equations to give you a comprehensive understanding of how this formula is derived.
Whether you’re a student studying calculus or just looking to expand your mathematical knowledge, this video is perfect for anyone interested in learning more about how formulas are created. After watching this video, you’ll have a deeper appreciation for the complexities of mathematics and how it applies to real-life scenarios.
Whether you’re a student studying calculus or just looking to expand your mathematical knowledge, this video is perfect for anyone interested in learning more about how formulas are created. After watching this video, you’ll have a deeper appreciation for the complexities of mathematics and how it applies to real-life scenarios.
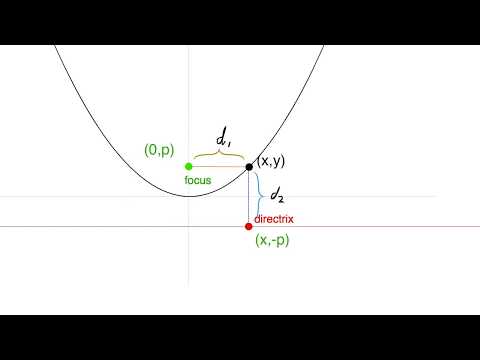
Equation of a Parabola, deriving the equation
How to Derive the Equations of Motion (Derivation)
How to Remember/Derive the Kinematics Equations
How to Derive Physics Equations : Physics Education
Deriving the SUVAT Equations of Motion - A Level Physics
Deriving Kinematic Equations - Kinematics - Physics
How to Derive Physics Equations
How to derive a formula for π
Ampere's Law | Ampere's Circuital Law | Electromagnetism | Class 12 Physics
Deriving Einstein's most famous equation: Why does energy = mass x speed of light squared?
Deriving the Dirac Equation
How to Derive the Quadratic Formula
Deriving the Wave Equation
DERIVE Equations of Motion | A Level Physics
Deriving 3 equations of motion (from v-t graph)
Derive Formulae | Algebra | Maths | FuseSchool
Deriving Hawking's most famous equation: What is the temperature of a black hole?
Cubic Formula Derivation
Deriving The Dirac Equation
Deriving 5 Kinematic Equations - Kinematics - Physics
How to Derive the Kinematic Equations of Motion *with Calculus*
Derive Equation of the Plane by Yourself!
How to derive the Equations of Motion - Kinematics | (Classical Mechanics)
Class 9 Science | Chapter 8 | Equation Of Motion Derivation | Motion | NCERT
Комментарии
 0:03:57
0:03:57
 0:04:12
0:04:12
 0:10:01
0:10:01
 0:01:34
0:01:34
 0:05:06
0:05:06
 0:08:20
0:08:20
 0:01:26
0:01:26
 0:01:00
0:01:00
 0:26:07
0:26:07
 0:36:49
0:36:49
 0:16:34
0:16:34
 0:04:49
0:04:49
 0:35:56
0:35:56
 0:05:03
0:05:03
 0:13:05
0:13:05
 0:03:37
0:03:37
 0:40:55
0:40:55
 0:00:18
0:00:18
 0:23:40
0:23:40
 0:06:37
0:06:37
 0:08:47
0:08:47
 0:04:33
0:04:33
 0:13:32
0:13:32
 0:11:16
0:11:16