filmov
tv
Proving the volume and the surface area of a sphere by using integrals

Показать описание
Proving the volume of a sphere with radius r 0:00
Proving the surface area of a sphere with radius r 6:14
For more calculus tutorials, check out my new channel "just calculus":
Proving the surface area of a sphere with radius r 6:14
For more calculus tutorials, check out my new channel "just calculus":
Visualizing the Volume of a Sphere Formula | Deriving the Algebraic Formula With Animations
Proving the volume and the surface area of a sphere by using integrals
The Volume of a Sphere - Numberphile
Why is the volume of a cone 1/3*pi*r^2*h? Here's a proof with the disc method! Calculus basics
Find the Volume of Any Shape Using Calculus
Volume of a pyramid is 1/3 the volume of a prism with the same base and height.
Volume of a Pyramid, simple explanation
Easy math. Deriving the formula for the volume of a cone #ibmath #igcse #ibexam #math #ipmath
The Legends of the Jews Volume 1 Part 37 - Digital Readers Club
Deriving the Volume of a Sphere
Volume of a Sphere: Three Different Derivations
A curious proof of cone's volume #SoME1 #SummerofMathExposition #3blue1Brown #geometry #cone
Volume of a Sphere (equation derived with calculus)
Volumes by Slicing (1 of 4: Proving the Volume formula integral)
Cylinder, Cone, and Sphere Volume
Why is the volume of a sphere V=4/3*pi*r^3? (calculus disk method)
Where Does The Volume of a Cylinder Formula Come From?
Volume of a Sphere | MathHelp.com
Volume of a Sphere
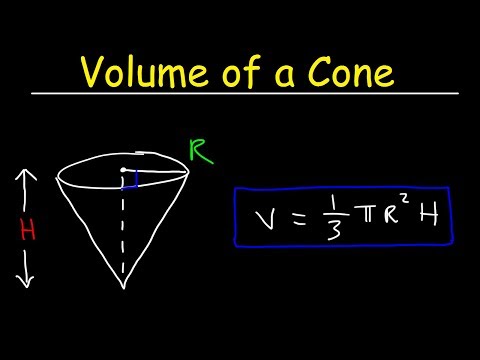
Volume of a Cone
Volume of a Cube
Proving The Volume of Sphere is 4/3 πr³
Find the Volume of Cones using Integral Calculus
Derive the Volume of a Sphere Using Integration (Disk Method)
Комментарии
 0:03:12
0:03:12
 0:13:41
0:13:41
 0:04:14
0:04:14
 0:07:10
0:07:10
 0:14:41
0:14:41
 0:01:52
0:01:52
 0:01:56
0:01:56
 0:00:48
0:00:48
 0:58:39
0:58:39
 0:12:29
0:12:29
 0:04:46
0:04:46
 0:08:09
0:08:09
 0:02:28
0:02:28
 0:08:22
0:08:22
 0:02:32
0:02:32
 0:05:58
0:05:58
 0:03:31
0:03:31
 0:01:57
0:01:57
 0:04:55
0:04:55
 0:01:32
0:01:32
 0:01:24
0:01:24
 0:06:11
0:06:11
 0:05:52
0:05:52
 0:04:00
0:04:00