Bernoulli's Water Tank | How Long Will It Take to Drain?

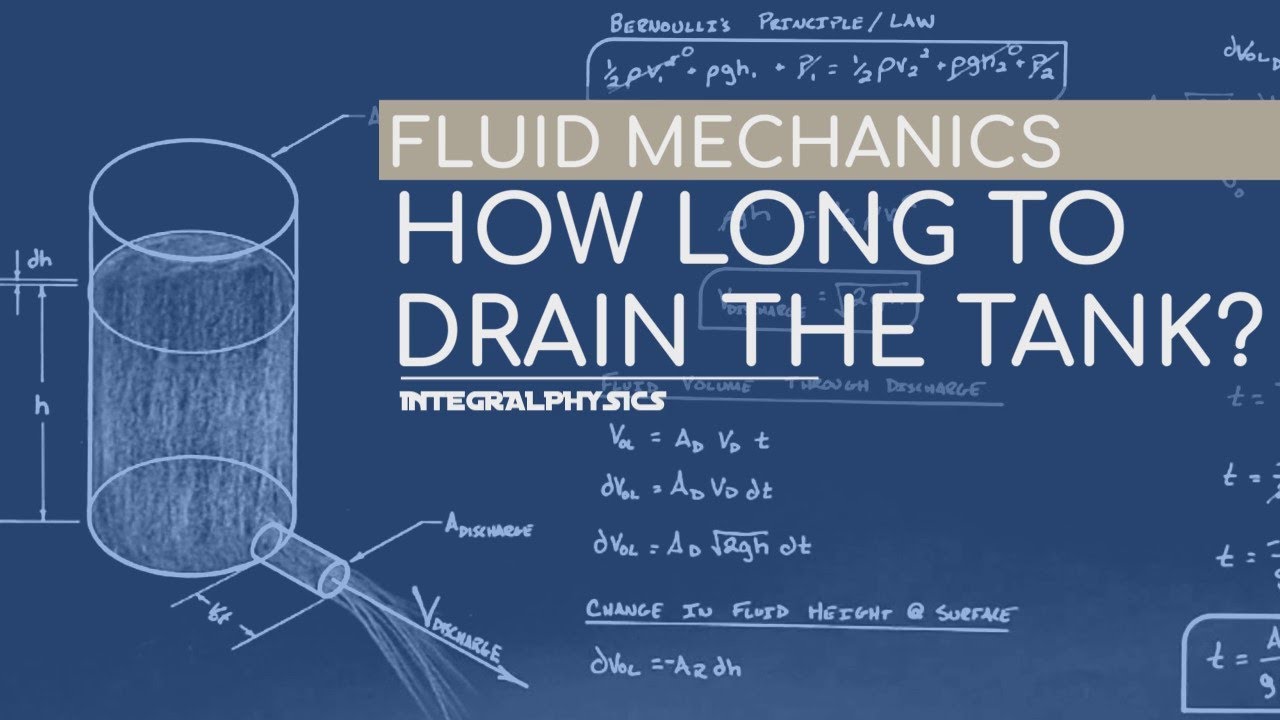
Having previously found the discharge velocity of fluid from the tank, we now solve for the total time to drain all the fluid, typically water, out of the tank.

This problem relies on the Bernoulli equation and a first order differential equation to solve for the time to empty the entire reservoir. By setting up a differential equation we go through the separation of variables and some otherwise pretty basic calculus. This solution is necessary because as the fluid level in the tank decreases, the rate at which fluid comes out of the tank will decrease.

This problem typically shows up in college physics, engineering, fluid mechanics courses and even calculus applications. It also appears in Project Lead the Way, Principles of Engineering, AP Physics and some high school physics curriculums.

[bkraj]

I'm searching videos with useful content and today I've found your channel.Bro you're awesome. You explained things pretty well without fancy animation and graphics. You got a unique style bro. You're going to rock youtube. Best wishes.🥳🥳🥳

[PTNLemay]

Thank you for this. I covered this in my fluid mechanics course, but I had forgotten pretty much all of it.

[klchin]

This is awesome application of mathematics and physics

[Jerrycaster]

That's amazing isn't it. The time for a tiny waterdrop to freefall from hight h to zero is given by: t= sqrroot(2h/g) so the time to drain is simply t multiplied by the ratio AR/AD.

[pedrohenriquecerqueira]

Very interesting and well done video!
If Bernoulli is an approximation and only applied for steady flows, how can we still use Bernoulli in this example if it's clearly a non steady flow as Velocity at any point x is a function of time? Thank you in advance

[mohamedbinsalman]

Hi, thanks so much for the video. I have a slight confusion. When you found the velocity using the Bernoullli equation, you assumed steady state flow and said that V1=0. But then, during the continuity equation, you wrote V1 as a differential, dh/dt. Does that actually make mathematical sense, or am I not getting the full picture. Because normally the tank drains unsteadly, and you need some differential to account for changes in downward velocity. Yet how can we do that when we already assume that V1 is 0.

[jelmerbijlsma]

Great explaination! Thanks a lot!
I'm struggeling with setting up a formula that tells me when I add water to the tank while it's draining, if the drain is big enough to keep up with the amount of water that is put in the tank. Could you do a video on that?

[vwcssuh]

Thanks for the video. Can you tell me how can I consider the friction loss in discharge pipe to this calculation

[qgyisku]

Great tutorial. Where can I find an example to determine the time when two open water tanks connected by a pipe reach the same water levels?

[jaydubouzet]

Please dont put background music when making discussion

[azharuddinghakhad]

Man your content deserves millions of subscribers but unfortunately people left studying science.

[cydroneguy]

Great Video! I have a question:

If the Reservoir had the shape of a funnel (or hopper), i.e. it's cross sectional area would decrease with decreasing height, how would that affect the discharge time?

I am assuming that the there will have to be an equation that relates the change of cross sectional area with respect to volume height, and then implement that into the solution presented in the video, but I am not quite sure how to go about solving it.

Any help would be much appreciated!

[tonijimenezbarcelo]

Hello Integral! I'm doing an investigation about water drainage, and if it's not a problem, can I ask you about your sources for the equations. I'm really stress out, and you'll save a young life from suffering more. Thanks in advance!

[hapless_]

Had to use subtitles as couldn't hear you over the thumping dance music.

[masoudkhoda]

nice, but should we considered any coefficient for that pipe? like orifice ?

[shubhamtalke]

Sir how will be the graph for emptying a tank of
height vs time
Velocity vs height

[simeonnewman]

Does the length of the discharge pipe have an effect?

[maxz]

Hi thanks so much for the video! Just one question, does it work for a square tank? Like area of reservoir is a square, say 1m x 1m

[brendangolledge]

I HAVE A CONCEPTUAL QUESTION PLZ HELP!

Hey I solved this problem by doing a differential equation to solve for h(t) (with help from wolfram) and I got the same result for the time.

However, I imagined, "what if the discharge area were the same as the tank area?" In that case, you get the same time as you would by dropping a ball off the top of the water column. But how can this physically work?

The initial velocity of the water coming out must be the same as the same as the ball dropped ball when it hits the ground. But if the discharge area were the same as the column area, that means the column would IMMEDIATELY gain a large velocity as soon as you opened the valve. Would that actually happen?

And then physically in the typical example, you'd expect the velocity to DECREASE as the tank drained. However, if the discharge area were virtually the same as the tank area, wouldn't that be like free-fall? In free-fall the initial velocity is 0 and then it accelerates.

Then you could imagine, "What if the discharge area were larger than the tank area?" In that case, it would seem like the discharge water would suck down the column of water faster than it would fall in free-fall. That doesn't seem right.

I guess one answer could be that if the discharge area were too large, then maybe the whole area of the discharge would not stay filled to the top with water, and air would get in and disturb the flow of the water. But if anybody has any other conceptual/practical ways of making me understand this better in the edge-case, that would be appreciated.

Suppose there were a really tall column of water (so that there was a lot of pressure at the bottom), and then the bottom cap on the column were made to instantly disappear with a magic wand. There would be a lot of pressure on that bottom surface the instant before the cap was removed, so I imagine that the water would come out with force in that instant. But how would that formerly pressurized water at the bottom force the water at the top of the column to also move down instantaneously with force? If I imagine tiny layers of water, the water at the bottom touching the air would come out fast because the water pressure above would be much greater than the air pressure below. Then when that tiny sliver of water moved, the same would happen to the sliver above, but at a somewhat reduced speed because of the lower pressure slightly higher up. So would there be a chain reaction of the water at the bottom instantly exploding down, with the water exploding down at reduced speed in proportion to the reduced height? Wouldn't that cause some kind of vacuum/cavitation if air didn't get mixed in? Or maybe a better conceptualization would be to say that the pressure in the water column would be immediately converted into velocity (or converted at the speed of sound), which would cause a velocity gradient, which would cause the water to have weird behavior like cavitation.

[target__iit]

People seeing this video after seeing alakh sir's fluid mechanics video, mark their attendance here ✋