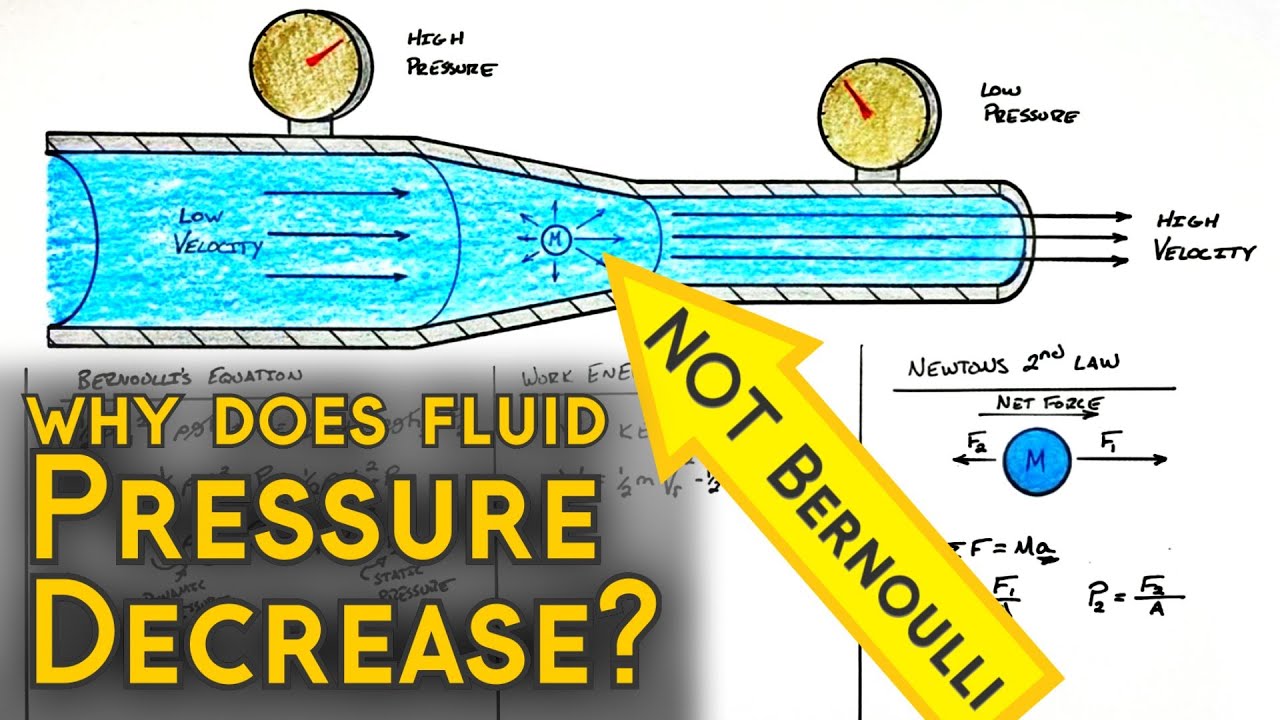
Why Does Fluid Pressure Decrease and Velocity Increase in a Tapering Pipe?

Bernoulli's Equation vs Newton's Laws in a Venturi

Often people (incorrectly) think that the decreasing diameter of a pipe correlates to a smaller volume and thus higher pressure. But the ideal gas law has no place in INCOMPRESSIBLE fluid flow.

Others try to explain the decrease in static pressure using Bernoulli's Principle, however, unless you have a VERY good handle on Bernoulli's, that is mostly a self supporting argument.

Back all the way up to Newton's 2nd Law to understand why there is a decrease in pressure in a pipe taper.

[nozack]

The explanation via Newton's 2nd law is a good one. However, what it clearly indicates, is that due to increasing velocity, there is necessarily a (positive to the right) acceleration, and therefore there must be a corresponding pressure gradient to explain this acceleration (to produce the necessary force). It does not state why the velocity (and hence acceleration) changed in the first place. That links you back to conservation of mass, or continuity.

So: Continuity explains why the velocity increases, and then via F= m(dv/dt) we can infer the necessity of a pressure gradient.

[joshuapowers]

Fun fact. In 1965 the Wood brothers used a fuel holding tank with this design which allowed them to dump 58 gallons of fuel into the tank of Jim Clark's Indy car in 15 seconds, while everyone else took 45 seconds to a minute. Thereby helping him secure the 1965 Indy 500 victory.

[doggy]

To think about this question intuitively, the pressure will stack up when water flows from a wide diameter to a smaller diameter. So the Pressure will be higher at the low-velocity part but remain unpressurized at the high-velocity part.
It's like pinching the soft water hose will let the water spray further. When doing so you will feel the force to pinch the hose, which will lead to pressurizing the original water flow.

[ytt]

I really don't know why nobody ever explains it like this, love it!!

[nathan]

I came here looking for a scientific reasoning to a magical ability im writing and I learned alot more then I thought I would lol.

[charlavenant]

I wish my physics and hydraulics profs had explained this in so much depth. Brilliant!

[mlvz]

Thank you for this clear answer !
It was not intuitive for me but after I saw the video I feel like it's intuitive :
It's logic that the fluid goes to a place where there is some resistance of the flow which generates an increase of pressure, and when it passes this place, there is no resistance anymore so the fluid is less under pressure.

[thomasherbig]

Outstanding. One step further would be to realize that it’s not the fluid going from slow to fast that causes the pressure to fall, but rather that the pressure difference accelerates the fluid from slow to fast. Same thing, but more clarity.

[EdwardChan.]

It finally clicked for me! Thanks a lot :)

Worth mentioning is another (wrong-ish) explanation that the increase in velocity decreases random motion, thus decreasing the pressure exerted on the pipe. However, Bernolli's principle only applies in streamline flow, i.e. no random motion.

[zaingujjar]

that was nice from you. that is what I got from you" imagine if you and your friend pushing an object to each other. Now the stronger one will push the object to the weak one" . Now just substitute your self with pressure. if the pressure on narrow side of the pipe was higher that particle wouldn't have moved to the narrow side

[PsychoWingedFish]

This explanation is actually very useful to understand physiology and blood pressure. There is a lot of tapering in blood vessels... Thanks!

[eldoctorramon]

Finally, the response to this question after all these years! :) :) Thanks!

[cienciabit]

Rotate it 90 degrees clockwise. Now we have a better intuition of pressure because of gravity. The key is "what is ahead?" The molecules at the top part (wide) are almost stuck since they have a small sink at the bottom, so they are pressing the walls. On the other hand, the molecules in the lower part (narrow) are almost free, because they have nothing ahead (below), so they are almost not pressing the walls.

[paulbfields]

I’m a practical tool and die designer and I build machine tools.. really enjoyed that which I already knew but just couldn’t explain it. “Work” is a concept many don’t understand. “Work” hardening is also another concept many can’t fathom. Unrelated here but then again aren’t they ?? Thank you.. I just subscribed.. Encore!!!

[brettbourgeois]

Thank you for the great explanation brother, I was in need of a quick brush up and luckily this video confirmed that I can retain SOME information. Just a heads up to anyone with epilepsy, just skip the the 11 second mark.

[live_free_or_perish]

Clever explanation. Better than I got in school 😊

[tomytran]

Thanks @INTEGRAL PHYSICS. Like @nozack5612 mentioned, the explanation through Newton's second is good but still left me missing an understanding of why the nozzle creates the pressure/velocity change. To round it out I offer this explanation (after researching more and thinking this through). My aha moment relies on considering the following: 1) static pressure fundamentally is a measure the fluid particles change in momentum to a surface (think walls of a container or more commonly the cross sectional area of a shape), and 2) continuity of mass flowrates between point 1 and 2 and the relation to incompressibility (i.e. the average number of particles in a given volume cannot change). Try to ignore the physical nozzle and imagine a setup where steady, incompressible flow goes from a larger diameter pipe to a smaller diameter pipe--the same fluid, the same density, the same mass flowrate. Take a cross section of the larger diameter pipe, there are more particle collisions (high static pressure) there because there are more particles flowing through that cross section at an instant in time. Now in a cross section of the smaller diameter pipe, with the same flow (i.e. flowrate) there are less particle collisions (low static pressure) because there are less particles flowing through that cross section at an instant in time. And since there are less particles in the cross section, to match the same mass flowrate as in the larger section the velocity must increase (i.e. the particles have to move faster through the pipe, otherwise that would mean the density is changing somewhere in the pipe!).

Okay so working under that knowledge, how does a steady, incompressible fluid flow go from a larger diameter pipe section to a smaller diameter pipe section? A nozzle! I think the counter-intuitive part is that we expect the fluid to be squeezed by the nozzle getting smaller and that means a larger pressure right? Nope. That only happens if we take the same mass of non-moving fluid from a larger volume into a smaller volume. However, I think that does happen when talking about supersonic nozzles or fluids that are moving REALLY fast (i.e. Mach numbers greater than 1) because compressibility changes, but I haven't studied enough yet.

That's my current understanding which still feels incomplete, but I hope that helps someone. I've been re-studying fluids for the FE exam which is why I'm here.

[Wildkat-]

The SR-71's engines ( P&W J-58's ) are a perfect example of this theory in action ...plus it actually uses supersonic air and transforms it to high pressure sub-sonic air ...!

[pst]

One mistake that many do is to consider the velocity variation as the cause of a pressure variation, while it is the opposite. Indeed, a change in velocity means an acceleration, which means a force applied. Usually, in a fluid the "forces", so what can cause a velociry variation, are mainly relered to pressure, viscosity, gravity.
The same for the aerodynamic of a wing: the profile of the wing imposes the bend of the fluid lines (since the air cannot compenetrate the solid body of the wing), which causes the modification of the pressure around the wing itself, which determines the forces on the wing (lift and drag) and the change in fluid velocity around the wing. Babinsky gave a good explanation for aerodynamics in his paper "how wings work". Obviously the viscosity plays also an important role, keeping the streamlines attached to the wing body (otherwise they would simply deflect at the wing nose and then remaining straight instead of curving).
What I suggest for flows in simple pipes is always to solve the continuity eq and the momentum eq of the NS equations in their integral form. Help you visualize the physics of the problem.

[UninstallingWindows]

The easiest way to explain it is by looking at what changes when the pipe gets narrower. The point where the pipe becomes narrower causes water molecules to impact the wall of the pipe at an angle, which will deflect the molecules to the middle. This will increase the pressure in the middle of the pipe. Higher pressure in the middle effectively funnels water molecules into the narrow pipe. Another way to think of it: "Take 3 marbles, and line them up next to each other. Sqeeze the 2 marbles at the end and see what happens to the middle one. It is flung outwards.