filmov
tv
What is a horizontal asymptote

Показать описание
👉 Learn all about asymptotes of a rational function. A rational function is a function, having a variable in the denominator. An asymptote is a line that the graph of a function approaches but never touches. There are the vertical, the horizontal and the slant/oblique asymptotes.
The vertical asymptote is a vertical line that the graph of a function approaches but never touches. To find the vertical asymptote(s) of a rational function, we set the denominator equal to 0 and solve for x.
The horizontal asymptote is a horizontal line which the graph of the function approaches but never crosses (though they sometimes cross them). A rational function has a horizontal asymptote of y = 0 when the degree of the numerator is less than the degree of the denominator. A rational function has a horizontal asymptote of y = c, (where c is the quotient of the leading coefficient of the numerator and that of the denominator) when the degree of the numerator is equal to the degree of the denominator. A rational function has no horizontal asymptote if the degree of the numerator is greater than the degree of the denominator.
A slant (oblique) asymptote usually occurs when the degree of the polynomial in the numerator is higher than the degree of the polynomial in the denominator. To find the slant asymptote of a rational function, we divide the numerator by the denominator using either long division or synthetic division. The quotient obtained when the numerator is divided by the denominator is the slant asymptote of the function.
Organized Videos:
✅ Find the Asymptotes of Rational Functions
✅ Find the Vertical and Horizontal Asymptotes of a Rational Function y=0
✅ Asymptotes of Rational Functions | Learn About
✅ Find the Asymptotes of a Rational Function with Trig
✅ Find the Asymptotes and Holes of a Rational Function
✅ Find the Slant Asymptotes of the Rational Function
Connect with me:
#asymptotes #functions #brianmclogan
The vertical asymptote is a vertical line that the graph of a function approaches but never touches. To find the vertical asymptote(s) of a rational function, we set the denominator equal to 0 and solve for x.
The horizontal asymptote is a horizontal line which the graph of the function approaches but never crosses (though they sometimes cross them). A rational function has a horizontal asymptote of y = 0 when the degree of the numerator is less than the degree of the denominator. A rational function has a horizontal asymptote of y = c, (where c is the quotient of the leading coefficient of the numerator and that of the denominator) when the degree of the numerator is equal to the degree of the denominator. A rational function has no horizontal asymptote if the degree of the numerator is greater than the degree of the denominator.
A slant (oblique) asymptote usually occurs when the degree of the polynomial in the numerator is higher than the degree of the polynomial in the denominator. To find the slant asymptote of a rational function, we divide the numerator by the denominator using either long division or synthetic division. The quotient obtained when the numerator is divided by the denominator is the slant asymptote of the function.
Organized Videos:
✅ Find the Asymptotes of Rational Functions
✅ Find the Vertical and Horizontal Asymptotes of a Rational Function y=0
✅ Asymptotes of Rational Functions | Learn About
✅ Find the Asymptotes of a Rational Function with Trig
✅ Find the Asymptotes and Holes of a Rational Function
✅ Find the Slant Asymptotes of the Rational Function
Connect with me:
#asymptotes #functions #brianmclogan
Комментарии
 0:03:35
0:03:35
 0:10:49
0:10:49
 0:02:08
0:02:08
 0:04:42
0:04:42
 0:03:54
0:03:54
 0:00:57
0:00:57
 0:02:36
0:02:36
 0:00:31
0:00:31
 0:02:14
0:02:14
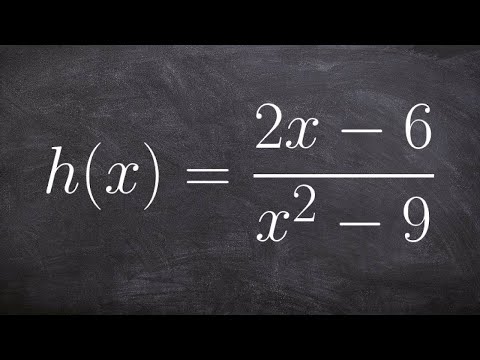 0:02:16
0:02:16
 0:08:04
0:08:04
 0:02:49
0:02:49
 0:00:56
0:00:56
 0:05:14
0:05:14
 0:11:22
0:11:22
 0:01:00
0:01:00
 0:03:15
0:03:15
 0:01:00
0:01:00
 0:00:36
0:00:36
 0:02:02
0:02:02
 0:10:50
0:10:50
 0:14:29
0:14:29
 0:00:20
0:00:20
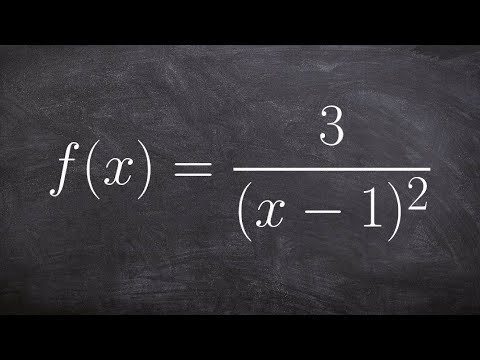 0:04:52
0:04:52