filmov
tv
Solving a Floor Value System

Показать описание
This video is about a floor value system
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FloorValueEquations
EXPLORE:
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FloorValueEquations
EXPLORE:
Solving a Floor Value System
Solving a floor value equation
Solving a Floor within Floor Equation
Solving a floor value equation. A challenge in algebra.
Solving a Quadratic Floor Equation
Solving a Quadratic Floor Equation
Solving An Easy Floor Value Equation (2⌊x⌋=3x)
Solving a nice floor equation for integers
Solving an equation with floor in it
I Solved a Floor and Ceiling Equation | Can you? 😉
How to Solve An Easy Floor Value Equation
Solving a crazy iterated floor equation.
Solving a nice floor equation
Reliable methodology for solving Floor, Fractional Part Equations
Solving an If-The Question Involving Floor Function | Evaluating the floor of an expression
Solution 63: Minimization with Floor and Ceiling
Solving Floor Equation Floor(x+1) +Floor(2x+2) = 13, Good estimate by removing Floor Brackets
Solve for x in the floor function equation
Solving a Canadian Math Olympiad Problem | Quadratic Equation with Floor of x | Olympiad Question
How I Solved An Equation with Floor Value | #numbertheory
Can you solve this Infinite Series with function of Floor Functions Summand
The most unexpected answer to a counting puzzle
Solution Set for Fractional Part Floor Equation {x} = Floor(sqrt(x/4 -1/3))
Find a solution set for the Trig floor equation floor(sin(8PI/7)) + floor(cos(7PI/8)) + 2 = 0
Комментарии
 0:10:25
0:10:25
 0:07:12
0:07:12
 0:08:26
0:08:26
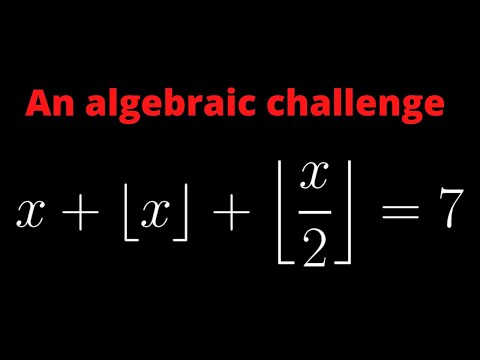 0:07:59
0:07:59
 0:13:28
0:13:28
 0:13:28
0:13:28
 0:04:59
0:04:59
 0:05:35
0:05:35
 0:15:25
0:15:25
 0:06:07
0:06:07
 0:04:59
0:04:59
 0:22:38
0:22:38
 0:08:21
0:08:21
 0:10:39
0:10:39
 0:04:39
0:04:39
 0:08:54
0:08:54
 0:12:00
0:12:00
 0:08:58
0:08:58
 0:11:30
0:11:30
 0:09:19
0:09:19
 0:03:01
0:03:01
 0:05:13
0:05:13
 0:05:36
0:05:36
 0:09:37
0:09:37