filmov
tv
Solving a floor value equation. A challenge in algebra.

Показать описание
This video is about a floor value equation that can be solved with little effort.
Floor value expressions,algebra,algebraic equations,SyberMath,algebraic manipulations,equations,substitution,Challenging Math Problems,Non-routine Math Problems,polynomial equations,an algebra challenge,algebraic identities,non-standard methods,symmetry,math,maths,mathematics,an algebraic challenge,floor value equations,A challenge in algebra.
Floor value expressions,algebra,algebraic equations,SyberMath,algebraic manipulations,equations,substitution,Challenging Math Problems,Non-routine Math Problems,polynomial equations,an algebra challenge,algebraic identities,non-standard methods,symmetry,math,maths,mathematics,an algebraic challenge,floor value equations,A challenge in algebra.
Solving a floor value equation
Solving a Floor Value Equation | #NumberTheory
Solving a Floor Value System
Solving a floor value equation. A challenge in algebra.
Solving a Quadratic Floor Equation
How to Solve An Easy Floor Value Equation
A Floor Value Equation
Solving a Floor within Floor Equation
SAT Prep||Unit 4||Radical, rational and absolute value equations
A floor value equation
Solving a Quadratic Floor Equation
Solving an equation with floor values
I Solved a Floor and Ceiling Equation | Can you? 😉
Solving An Easy Floor Value Equation (2⌊x⌋=3x)
Floor equation
A Floor Value Equation (x^2-⌊x⌋-2=0)
A quadratic floor equation.
An equation with floor values! An algebraic adventure in equations and inequalities...
Floor equation for the win
A Floor and Ceiling Equation, Floor(x-Ceil(x/2))=3
Algebra: Equation with Floor and Ceiling
Solving A Floor Equation | Special Functions
Solve for x in the floor function equation
Solving a nice floor equation for integers
Комментарии
 0:07:12
0:07:12
 0:07:12
0:07:12
 0:10:25
0:10:25
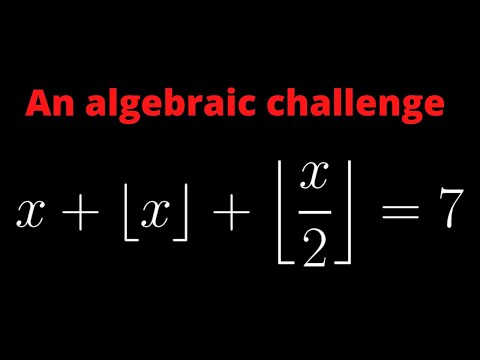 0:07:59
0:07:59
 0:13:28
0:13:28
 0:04:59
0:04:59
 0:12:25
0:12:25
 0:08:26
0:08:26
 0:54:31
0:54:31
 0:12:25
0:12:25
 0:13:28
0:13:28
 0:02:24
0:02:24
 0:06:07
0:06:07
 0:04:59
0:04:59
 0:12:31
0:12:31
 0:09:38
0:09:38
 0:13:27
0:13:27
 0:09:15
0:09:15
 0:03:34
0:03:34
 0:07:13
0:07:13
 0:04:39
0:04:39
 0:00:40
0:00:40
 0:08:58
0:08:58
 0:05:35
0:05:35