filmov
tv
Solving a nice floor equation for integers

Показать описание
We solve the equation: floor(x/4)+floor(x/2)=27 for integer x.
#math,#algebra,#equation,numbers,integration,differentiation,derivative,integral,math elite,mathelite,maths,mathematics,calculus
#math,#algebra,#equation,numbers,integration,differentiation,derivative,integral,math elite,mathelite,maths,mathematics,calculus
Solving a nice floor equation
a nice iterated floor equation.
A quadratic floor equation.
A Nice Equation on Floor Functions! || High School Math
Solving a Floor within Floor Equation
Floor equation
Solving a crazy iterated floor equation.
a floor equation.
Simplify & Solve Rational Equations & Expressions like a Pro!
Solving a floor value equation
Solving a floor value equation. A challenge in algebra.
A really nice equation involving the fractional part of a variable.
Solving A Floor Equation | Special Functions
Solving a Quadratic Floor Equation
Algebra: Crazy Nested Floor Equation
a good place for a floor equation.
Quadratic Floor Equation
A ceiling and floor equation
An equation with floor values! An algebraic adventure in equations and inequalities...
Thanks for the floor equation nice viewer!
A 'quick' floor exponent equation
Algebra: Equation with Floor and Ceiling
How to satisfy this floor equation?
How to Solve An Easy Floor Value Equation
Комментарии
 0:08:21
0:08:21
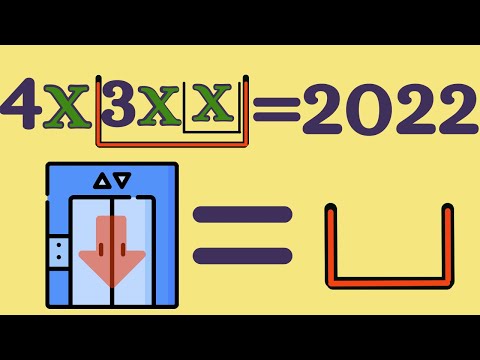 0:06:52
0:06:52
 0:13:27
0:13:27
 0:10:51
0:10:51
 0:08:26
0:08:26
 0:12:31
0:12:31
 0:22:38
0:22:38
 0:15:11
0:15:11
 0:42:26
0:42:26
 0:07:12
0:07:12
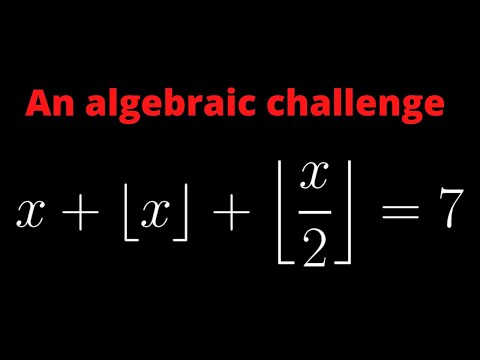 0:07:59
0:07:59
 0:12:59
0:12:59
 0:00:40
0:00:40
 0:13:28
0:13:28
 0:13:54
0:13:54
 0:10:35
0:10:35
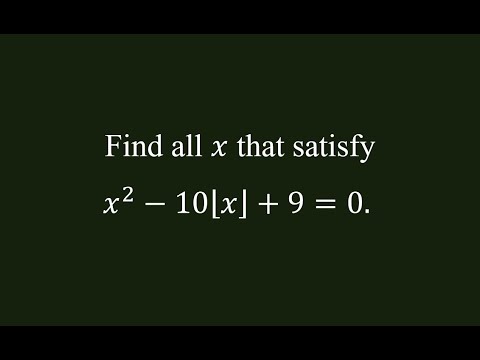 0:03:29
0:03:29
 0:08:26
0:08:26
 0:09:15
0:09:15
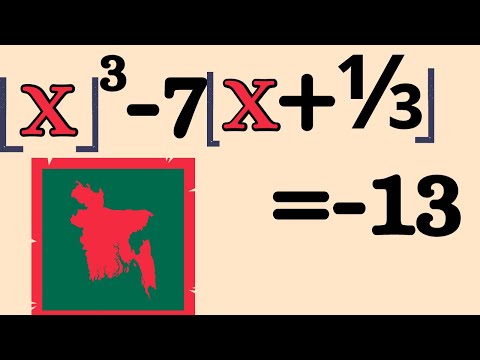 0:07:00
0:07:00
 0:09:50
0:09:50
 0:04:39
0:04:39
 0:11:43
0:11:43
 0:04:59
0:04:59