filmov
tv
Solving a Quadratic Floor Equation

Показать описание
This video is about a floor equation
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FloorValueEquations
EXPLORE:
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FloorValueEquations
EXPLORE:
Solving a Quadratic Floor Equation
A quadratic floor equation.
Solving a Quadratic Floor Equation
Quadratic ceiling floor inequality
CMO 1999 | A quadratic floor function equation
Quadratic Floor Equation
A Quadratic Equation With the Floor Function | Canadian National Mathematical Olympiad 1999
a floor equation.
A rectangular floor area can be completely tiled with 200 square tiles.#Class10maths @classdemics
Solving a Canadian Math Olympiad Problem | Quadratic Equation with Floor of x | Olympiad Question
A floor value equation
Solving An Easy Floor Value Equation (2⌊x⌋=3x)
Similar To Quadratic Floor Equation
another floor equation!
A system of equations with the floor function.
Solving Quadratic Trigonometric Equations
when an equation has the floor and the fractional part functions
Floor Plan With Quadratic Equation (see description)
Solving Problems Involving Quadratic Equations and Rational Algebraic Equations
Ex: Quadratic Equation App - Determine When an Object Hits the Ground (Factoring)
Floor Plan With Quadratic Equation
Quadratic Equation Area Word Problem
Equation involving Floor of Decreasing Linear Function Set equal to Floorless Quadratic Expression
A really interesting floor problem!
Комментарии
 0:13:28
0:13:28
 0:13:27
0:13:27
 0:13:28
0:13:28
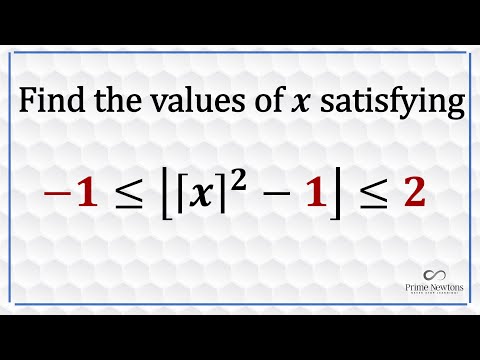 0:08:26
0:08:26
 0:09:32
0:09:32
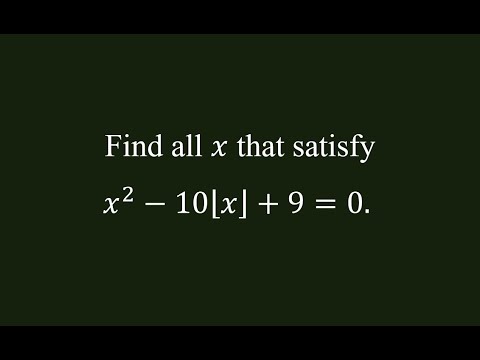 0:03:29
0:03:29
 0:09:34
0:09:34
 0:15:11
0:15:11
 0:20:24
0:20:24
 0:11:30
0:11:30
 0:12:25
0:12:25
 0:04:59
0:04:59
 0:04:31
0:04:31
 0:08:18
0:08:18
 0:12:32
0:12:32
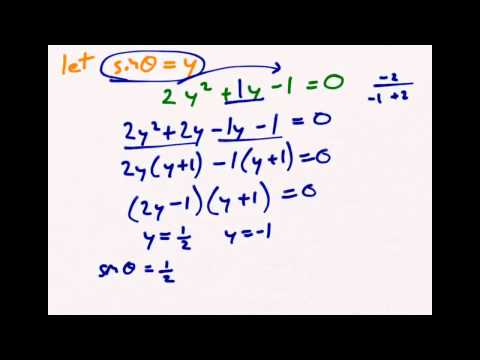 0:05:53
0:05:53
 0:05:55
0:05:55
 0:06:46
0:06:46
 0:25:20
0:25:20
 0:04:16
0:04:16
 0:05:31
0:05:31
 0:05:23
0:05:23
 0:11:02
0:11:02
 0:08:24
0:08:24