filmov
tv
Solving a nice floor equation

Показать описание
So today we will be solving a nice floor equation . these type of problem are really nice to solve and satisfying .
So if you have any other method other than mine or else if you have any other question that you think I should try you can Email me or else you can send it to me on my Instagram .
My Email address
My Instagram account
A huge thanks to Vincent Rubinetti for the background Music
#math algebra #mathematics
So if you have any other method other than mine or else if you have any other question that you think I should try you can Email me or else you can send it to me on my Instagram .
My Email address
My Instagram account
A huge thanks to Vincent Rubinetti for the background Music
#math algebra #mathematics
Solving a nice floor equation
a nice iterated floor equation.
A quadratic floor equation.
A Nice Equation on Floor Functions! || High School Math
Solving a Floor within Floor Equation
Floor equation for the win
Floor equation
Solving a floor value equation
Pay small, Clean big: One Sachet Solution for a Full Bottle of Floor Cleaner
Solving a crazy iterated floor equation.
a floor equation.
Solving a floor value equation. A challenge in algebra.
Solving A Floor Equation | Special Functions
A really nice equation involving the fractional part of a variable.
Solving a Quadratic Floor Equation
Quadratic Floor Equation
a good place for a floor equation.
A ceiling and floor equation
Thanks for the floor equation nice viewer!
An equation with floor values! An algebraic adventure in equations and inequalities...
Algebra: Equation with Floor and Ceiling
Solving an equation with floor in it
How to satisfy this floor equation?
How to Solve An Easy Floor Value Equation
Комментарии
 0:08:21
0:08:21
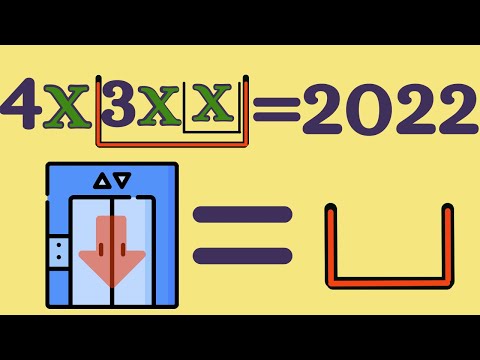 0:06:52
0:06:52
 0:13:27
0:13:27
 0:10:51
0:10:51
 0:08:26
0:08:26
 0:03:34
0:03:34
 0:12:31
0:12:31
 0:07:12
0:07:12
 0:00:37
0:00:37
 0:22:38
0:22:38
 0:15:11
0:15:11
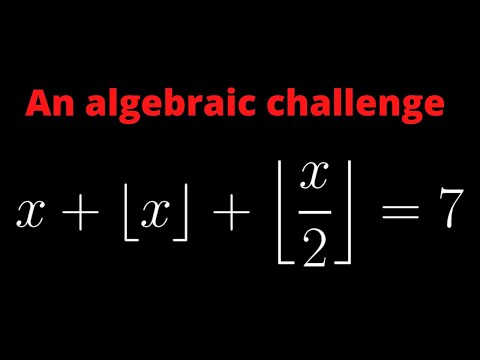 0:07:59
0:07:59
 0:00:40
0:00:40
 0:12:59
0:12:59
 0:13:28
0:13:28
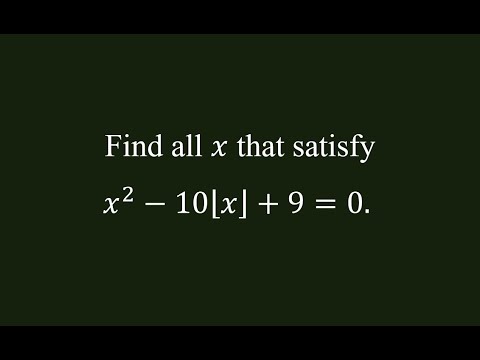 0:03:29
0:03:29
 0:10:35
0:10:35
 0:08:26
0:08:26
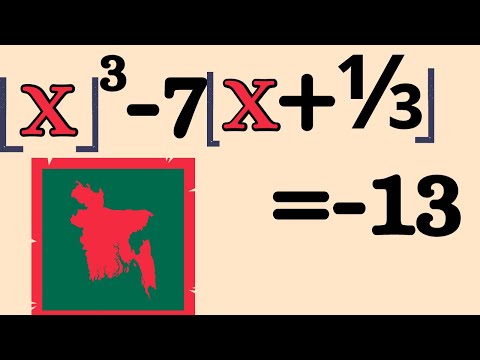 0:07:00
0:07:00
 0:09:15
0:09:15
 0:04:39
0:04:39
 0:15:25
0:15:25
 0:11:43
0:11:43
 0:04:59
0:04:59