filmov
tv
Puedes calcular el área sombreada

Показать описание
#AcademiaInternet, #LaPracticaHaceAlMaestro
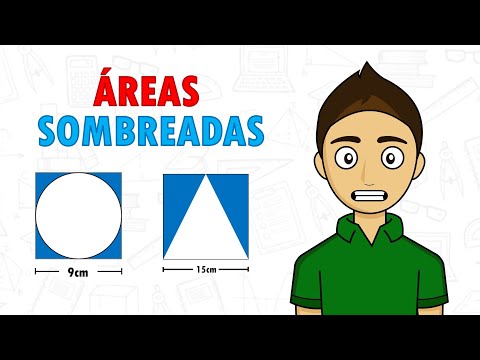
ÁREAS SOMBREADAS Super fácil - Para principiantes
Puedes calcular el área sombreada en 45 segundos
¿Puedes calcular el área sombreada? | 🤔🤯😱
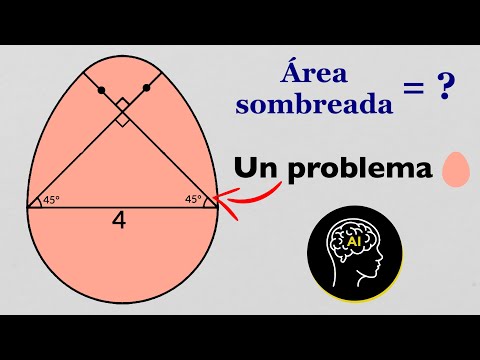
¿Puedes calcular el área sombreada? | 🤓👉🥚
¿Puedes calcular el área sombreada?
Área sombreada - debes resolverlo en 30 segundos
¿Puedes calcular el área sombreada? | 🤔🤷♂️🤓
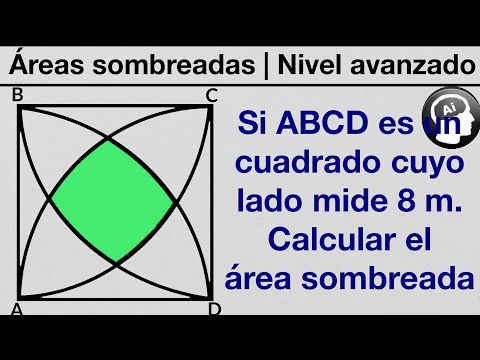
¿Puedes calcular el area sombreada conociendo solo el lado del cudradado? | NAVETA
¿Puedes calcular el área sombreada? | 🧠🤯🤓
Puedes calcular el área sombreada
¿Puedes calcular el área sombreada?
Puedes calcular el área sombreada en 1 minuto ~ desafío geométrico
Áreas sombreadas
¿Puedes calcular el area sombreada de la figura?
¿Puedes calcular el area sombreada con los datos mostrados? | [artificios geometricos]
¿Puedes calcular el area sombreada usando artificos geometricos?
¿Puedes calcular el areas sombreada? | SOLUCION GEOMETRICA
Puedes calcular el AREA SOMBREADA😎semicirculo Pegado a un Triangulo
¿Puedes calcular el área sombreada?
¿Puedes calcular el área sombreada? ¿Solamente 1 de cada 100 puede resolverlo?
¿Puedes calcular el Área sombreada? Área de región Sombreada | Área de figuras compuestas
La respuesta está en tu corazón. Puedes calcular el área sombreada
Área de una región sombreada. Explicación rápida. #math #matematicas #Grajeda
Puedes calcular el area sombreada (Happy Pi Day!)
Комментарии
 0:07:48
0:07:48
 0:00:49
0:00:49
 0:06:23
0:06:23
 0:06:06
0:06:06
 0:08:23
0:08:23
 0:00:55
0:00:55
 0:06:29
0:06:29
 0:07:28
0:07:28
 0:05:01
0:05:01
 0:03:07
0:03:07
 0:03:40
0:03:40
 0:02:03
0:02:03
 0:01:01
0:01:01
 0:08:23
0:08:23
 0:07:39
0:07:39
 0:06:57
0:06:57
 0:15:43
0:15:43
 0:07:36
0:07:36
 0:12:01
0:12:01
 0:06:14
0:06:14
 0:06:08
0:06:08
 0:02:50
0:02:50
 0:00:56
0:00:56
 0:03:01
0:03:01