filmov
tv
The Squeeze Theorem of Calculus Explained
Показать описание
This tutorial delves into the Squeeze Theorem, a fundamental concept in calculus that offers a powerful tool for evaluating limits, especially when direct substitution is not possible. Aimed at students, educators, or anyone looking to enhance their understanding of mathematical analysis, this video simplifies the theorem, making it accessible and easy to grasp for viewers at all levels.
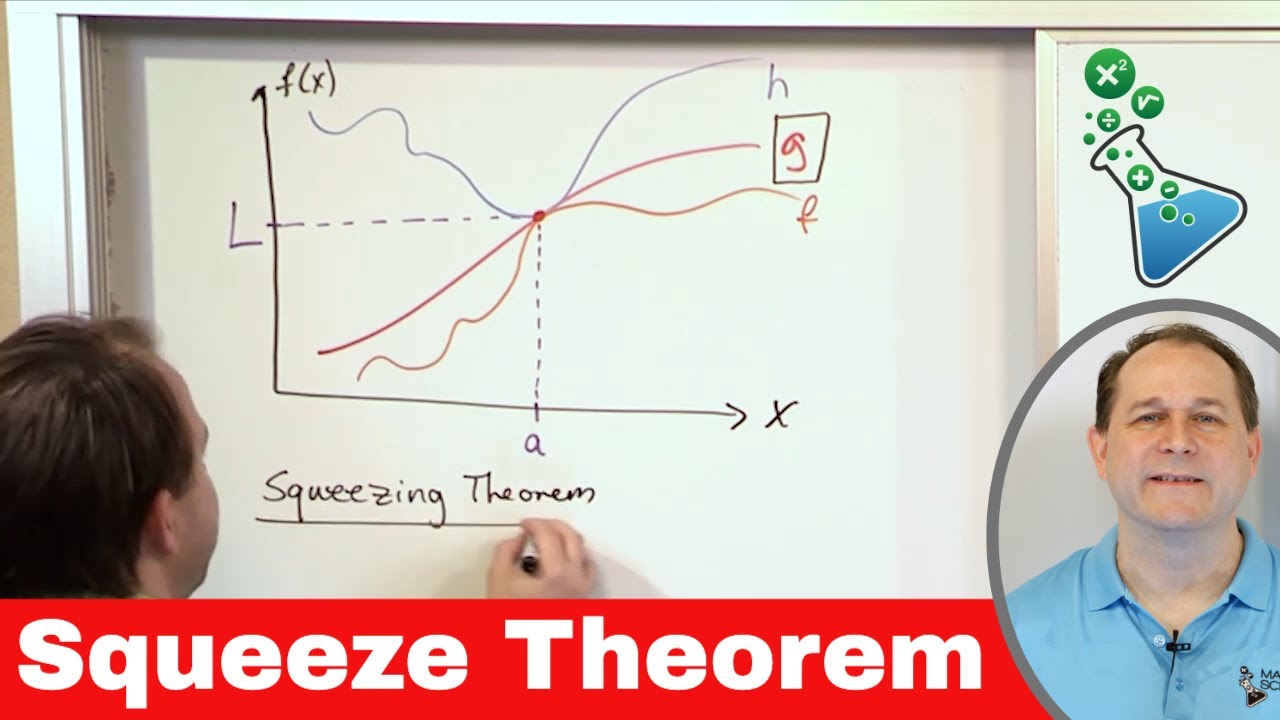
The Squeeze Theorem, also known as the Sandwich Theorem or Pinching Theorem, is based on the principle that if a function is bounded by two other functions that have the same limit at a certain point, then the function of interest must also converge to that same limit.
Through detailed examples, the tutorial demonstrates how to apply the Squeeze Theorem to solve limit problems involving trigonometric, polynomial, and other types of functions. Viewers will learn how to identify situations where the theorem can be effectively used and see step-by-step how to set up the bounding functions.
Additionally, the video highlights common pitfalls in applying the Squeeze Theorem and offers tips for avoiding these mistakes. By the end of this tutorial, viewers will have a solid grasp of using the Squeeze Theorem to find limits, enhancing their problem-solving skills in calculus. Join us to unlock the potential of this essential analytical tool.
The Squeeze Theorem, also known as the Sandwich Theorem or Pinching Theorem, is based on the principle that if a function is bounded by two other functions that have the same limit at a certain point, then the function of interest must also converge to that same limit.
Through detailed examples, the tutorial demonstrates how to apply the Squeeze Theorem to solve limit problems involving trigonometric, polynomial, and other types of functions. Viewers will learn how to identify situations where the theorem can be effectively used and see step-by-step how to set up the bounding functions.
Additionally, the video highlights common pitfalls in applying the Squeeze Theorem and offers tips for avoiding these mistakes. By the end of this tutorial, viewers will have a solid grasp of using the Squeeze Theorem to find limits, enhancing their problem-solving skills in calculus. Join us to unlock the potential of this essential analytical tool.
Комментарии
 0:10:43
0:10:43
 0:07:11
0:07:11
 0:10:59
0:10:59
 0:10:49
0:10:49
 0:06:02
0:06:02
 0:06:59
0:06:59
 0:15:23
0:15:23
 0:08:05
0:08:05
 0:05:44
0:05:44
 0:03:09
0:03:09
 0:03:44
0:03:44
 0:10:25
0:10:25
 0:15:18
0:15:18
 0:11:28
0:11:28
 2:14:36
2:14:36
 0:00:59
0:00:59
 0:05:19
0:05:19
 0:11:40
0:11:40
![[Calculus] Squeeze Theorem](https://i.ytimg.com/vi/EzVO6E1ZqLc/hqdefault.jpg) 0:08:20
0:08:20
 0:05:30
0:05:30
 0:01:41
0:01:41
 0:05:35
0:05:35
 0:10:21
0:10:21
 0:12:43
0:12:43