filmov
tv
Limits of Oscillating Functions and the Squeeze Theorem

Показать описание
Description:
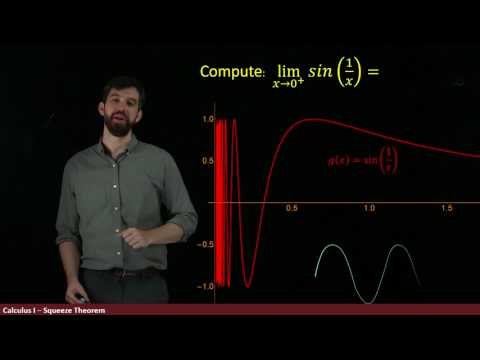
Some functions start oscillating "infinitely" quickly near a point. Limits at those points don't exist if the oscillations have a nonzero height. However, of the function both oscillates and goes down towards zero, the Squeeze Theorem lets us compute the limit too.
Learning Objectives:
1) Compute the limit of a function near a point with "infinite" oscillations
2) Apply the squeeze theorem - carefully verifying the assumptions - to compute limits of functions such as xsin(1/x) near 0.
Now it's your turn:
1) Summarize the big idea of this video in your own words
2) Write down anything you are unsure about to think about later
3) What questions for the future do you have? Where are we going with this content?
4) Can you come up with your own sample test problem on this material? Solve it!
Learning mathematics is best done by actually DOING mathematics. A video like this can only ever be a starting point. I might show you the basic ideas, definitions, formulas, and examples, but to truly master calculus means that you have to spend time - a lot of time! - sitting down and trying problems yourself, asking questions, and thinking about mathematics. So before you go on to the next video, pause and go THINK.
This video is part of a Calculus course taught by Dr. Trefor Bazett at the University of Cincinnati.
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
Some functions start oscillating "infinitely" quickly near a point. Limits at those points don't exist if the oscillations have a nonzero height. However, of the function both oscillates and goes down towards zero, the Squeeze Theorem lets us compute the limit too.
Learning Objectives:
1) Compute the limit of a function near a point with "infinite" oscillations
2) Apply the squeeze theorem - carefully verifying the assumptions - to compute limits of functions such as xsin(1/x) near 0.
Now it's your turn:
1) Summarize the big idea of this video in your own words
2) Write down anything you are unsure about to think about later
3) What questions for the future do you have? Where are we going with this content?
4) Can you come up with your own sample test problem on this material? Solve it!
Learning mathematics is best done by actually DOING mathematics. A video like this can only ever be a starting point. I might show you the basic ideas, definitions, formulas, and examples, but to truly master calculus means that you have to spend time - a lot of time! - sitting down and trying problems yourself, asking questions, and thinking about mathematics. So before you go on to the next video, pause and go THINK.
This video is part of a Calculus course taught by Dr. Trefor Bazett at the University of Cincinnati.
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
Комментарии
 0:06:59
0:06:59
 0:02:23
0:02:23
 0:06:45
0:06:45
 0:03:20
0:03:20
 0:06:02
0:06:02
 0:05:16
0:05:16
 0:03:02
0:03:02
 0:09:52
0:09:52
 0:04:01
0:04:01
 0:00:48
0:00:48
 0:03:49
0:03:49
 0:07:48
0:07:48
 0:02:17
0:02:17
 0:03:15
0:03:15
 0:27:16
0:27:16
 0:04:13
0:04:13
 0:06:37
0:06:37
 0:07:56
0:07:56
 0:30:13
0:30:13
 0:04:19
0:04:19
 0:20:43
0:20:43
 0:03:36
0:03:36
 0:05:18
0:05:18
 0:02:38
0:02:38