❖ The Squeeze Theorem for Limits, Example 3 ❖

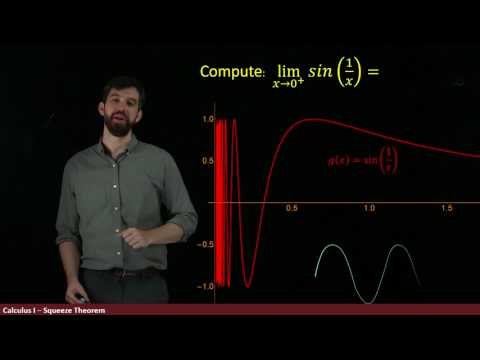
The Squeeze Theorem for Limits, Example 3. This squeeze theorem problem is a little more tricky since we have to produce the small and large function to bound our original function. It is NOT completely mechanical; some thought is needed on this one!
In order to perform this (rather typical) type of limit involving the Squeeze Theorem we need to bound our limiting function. If you have this type of example involving sine or cosine and a power function, typically the power function will be used to help bound so be on the lookout for that!

[patrickjmt]

Hi all! Wanna help a Youtube education OG? Please post comments, questions and anything else on your mind in the comment section! so, don’t forget to LIKE, THUMBS UP, and SUBSCRIBE! I’d appreciate it greatly as it helps me :)

[diamondpearl]

I didn't understand the squeeze theorem for the longest time ever even though I was doing some complex calculus. This video did for me in five minutes what my college calculus teacher couldn't do in 2 semesters.

[mmarshall]

"Life is a little more difficult" yaa AGREED haha

[vprovost]

Hi Patrick!
I just wanted to let you know I've been watching you for a long time and for the reason that your videos are the highest quality out there on math subjects hands down. Thank you for dedicating your time.

Sincerely, a grateful student

[alexc]

My uni book has about one sentence describing squeeze theorem - 0 explanation on how to do it, etc.

Putting it in the form of an inequality really helped clear things up when only given an equation of a function, vs. graphs, etc. Thanks a lot, keep up the amazing work :) 

[omkars]

So much more helpful than a textbook explanation.  THanks!

[JayTee]

Thanks a lot! You have no idea how much you've helped.

[hibakhan]

I used your videos for all three of my university math classes (discrete math, linear algebra, and now calc) and I haven't come across better videos!!! Thankyou so much man

[mkg]

Thanks again, can't put into words how much you have helped me, i went to so many places no one was helping me, just thought let me youtube it and here i got it.I am not good in math but now i feel there are no bad students just bad teacher and you are simply outstanding.

[mvahabza]

I've sat in class for 8 hours a day for around 6 weeks now and I learned more from your three sandwich theorem videos than my professor taught me over that period of time. If only he played your videos and kept his mouth shut the entire semester.

[hazardousnermz]

i have this prof who over complicates life but this made SOOO much sense after you explained it! the joy of understanding math :') Thanks a ton

[SaadNaeem]

@patrickJMT life saver was stuck at sandwich theorem for quiet some time almost gave up on it until saw this video makes sense now thanks a lot god bless you

[afro]

Your videos are a life saver, many blessings.

[chadeptus]

Great video! I came to a halt when I received undefined.

[tulipbaby]

This was really helpful! Now I understand why I'm doing these steps.

Your videos are always so clear! I know you hear this all this time, but your the reason why I am passing Calculus 1. Thank you so much!

[dashakrayushkina]

If only you were my calculus professor. Thanks to your vids I might actually pass my midterm now!

[roydaneker]

Better than Khan Academy Thank you so much.

[patrickjmt]

@hpeselyk well, your teacher ' warmed you up ' for me

[mulakonawa]

It's 10years later and you still help someone 👏🏾

[andynonymous]

Ok so:
1. find the range of f(x) without applying any transformations in y values if it was in a graph
2.put it in this form: lowest range number ≤ f(x) ≤ highest range number
3. apply the transformations to the left and right side of the inequality so that it reflects the range of the graph after applying transformations on the y values
ex: 2 x lowest range number ≤ 2 x f(x) ≤ 2 x highest range number
4. apply the limit on the middle function to the functions on the left and right side of the inequality
5. solve the limits
6. if the 2 outer equations are equal then the inner one equals the same.

I don't know if I explained that well but that's what I got from this video. Thanks, I think I get it now :)
I'll definitely be back- like and subbed