Application of Markov Chain/Process | Transition Matrix | Steady state vectors | Linear Algebra

Application of Markov Chain/Process | Transition Matrix | Steady state vectors | Linear Algebra

----------------------------------------------------------------------------------

In this lecture we will learn problems based on "The application of Markov process or Markov Chain, Transition Matrix, Steady State Vector, with two(2) exercise problems" concerned with the course "Linear Algebra" written by Bernard Kolman and David R Hill "8th" edition.

---------------------------------------------------------------------

#MarkovProcess
#MarkovChain
#TransitionMatrix
#SteadyStateVector
#ProbabilityVector
#LinearAlgebra
#EngineerArif
#CalculusandMathematicslearning

---------------------------------------------------------------------

for complete playlist of this course "Linear Algebra " click on the below link:

------------------------------------------------------------------------

chapters for this video:
00:00 (Introduction + Concept)
00:21 (Question # 01) part (a) Find the transition Matrix
04:00 (Question # 01) part (b) Find the probability of the rat passing through door A on Thursday (3rd day of starting experiment)
11:46 (Question # 01) part (c) Find the Steady state vector for this Markov Process?
15:13 (Question # 02) Write Transition Matrix for this Markov Process?
17:10 (Question # 02) What percentage of those receiving the current letter can be expected to order a subscription?

---------------------------------------------------------------------------------

Question # 09 statement:
----------------------------------------
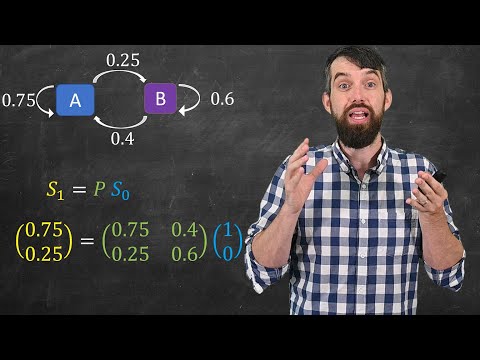
"A behavioural psychologist places a rat each day in a cage with two doors; A and B.The rat can go through door A, where it receives an electric shock, or go through door B, where it receives some food. A record is made of the door through which the rat passes. At the start of the experiment, on a Monday, the rat is equally likely to go through door A as through door B. After going though door A, and receiving a shock, the probability of going through same door on the next day is 0.3. After going through door B, and receiving food, the probability of going through same door on the next day is 0.6.
a) Find the transition matrix for this Markov Process
b) Find the probability of the rat going though door A on Thursday (the third day after starting the experiment)
c) Find the steady state vector for this process

Question # 10 statement:
----------------------------------------
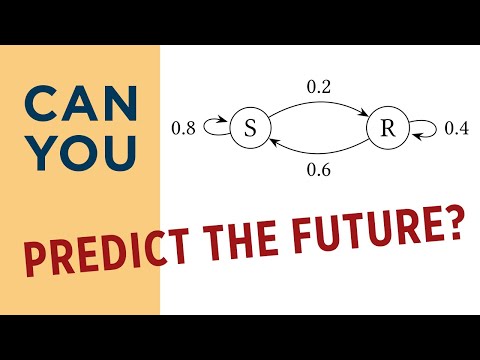
The subscription department of magazine sends out a letter to a large mailing list inviting subscriptions for the magazine. Some of the people receiving this letter already subscribe to magazine, while others do not. From this mailing list, 60% of those who already subscribe will subscribe again, while 25% of those who do not now subscribe will subscribe.
a) Write Transition Matrix for this Markov Process
b) On the last letter it was found that 40% of those receiving it, ordered a subscription. What percentage of those receiving the current letter can be expected to order a subscription?

---------------------------------------------------------------------------------

Tags:
---------
Markov Chain
Markov Process
Markov Matrix
Stochastic Matrix
Probability Matrix
Transition Matrix
Probability Vector
State Vector
Steady State Vector
Initial State Vector
Linear Algebra
Find steady State Vector for the given regular matrices?