filmov
tv
Introducing Markov Chains

Показать описание
A Markovian Journey through Statland [Markov chains probability
animation, stationary distribution]
animation, stationary distribution]
Introducing Markov Chains
Markov Chains Clearly Explained! Part - 1
Intro to Markov Chains & Transition Diagrams
Origin of Markov chains | Journey into information theory | Computer Science | Khan Academy
L24.2 Introduction to Markov Processes
Markov Chains - Short Introduction | David Kozhaya
Markov Chain Monte Carlo (MCMC) : Data Science Concepts
Markov Decision Processes - Computerphile
Introducing Markov Chains
Stats 102C Lesson 5-1 Introducing Markov Chains (Lecture 1)
Markov Chains & Transition Matrices
Introduction to Markov Chains
Introduction to Markov Chains 1of 2
Introduction to Markov Chain
Random walks in 2D and 3D are fundamentally different (Markov chains approach)
Prob & Stats - Markov Chains (1 of 38) What are Markov Chains: An Introduction
Introduction: MARKOV PROCESS And MARKOV CHAINS // Short Lecture // Linear Algebra
Introduction to Bayesian statistics, part 2: MCMC and the Metropolis–Hastings algorithm
Markov Chains : Data Science Basics
Chains Excite Me: Introduction to Markov Chains
Introduction to Markov Chain Modelling
Introduction To Markov Chains | Markov Chains in Python | Edureka
MARKOV CHAINS - Introduction
Part I. Introduction to Markov Chains
Комментарии
 0:04:46
0:04:46
 0:09:24
0:09:24
 0:11:25
0:11:25
 0:07:15
0:07:15
 0:02:09
0:02:09
 0:04:29
0:04:29
 0:12:11
0:12:11
 0:17:42
0:17:42
 0:03:59
0:03:59
 0:48:37
0:48:37
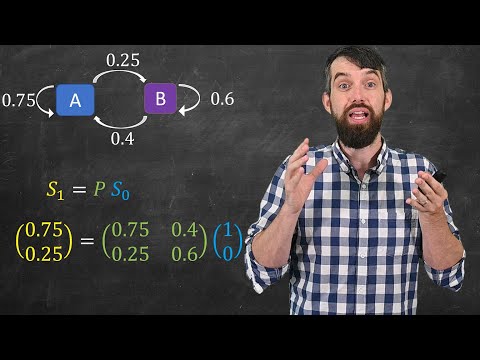 0:06:54
0:06:54
 0:14:33
0:14:33
 0:34:20
0:34:20
 0:09:44
0:09:44
 0:18:22
0:18:22
 0:12:50
0:12:50
 0:16:00
0:16:00
 0:08:14
0:08:14
 0:10:24
0:10:24
 0:06:27
0:06:27
 0:25:09
0:25:09
 0:26:44
0:26:44
 0:07:23
0:07:23
 0:41:56
0:41:56