filmov
tv
Solving a Math Olympiad Question | Solving a System of Equations Equation For Integer Solutions
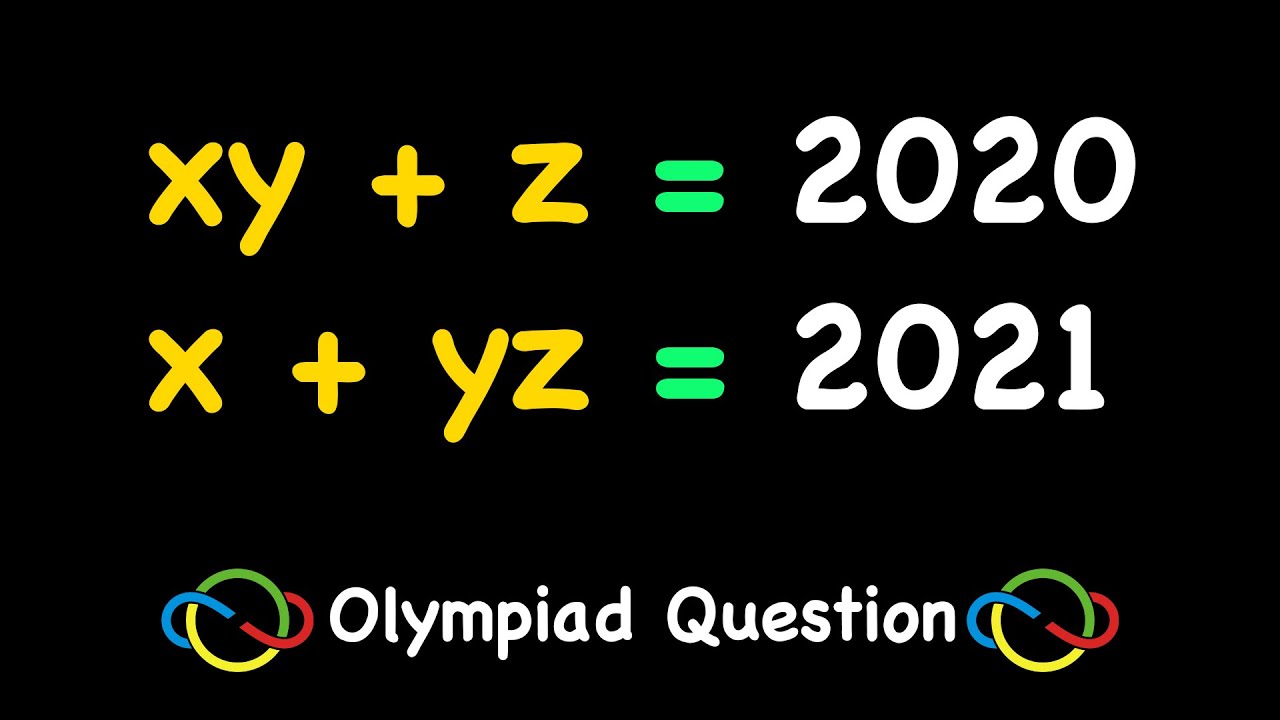
Показать описание
🔴 Solving a Math Olympiad Question | Solving a System of Equations Equation For Integer Solutions | A Math Olympiad Problem With Integer Solutions
Hey there.
In this video, we want to solve another math olympiad question, in which we have a system of equations with integer solutions. We are given
xy+z=2020
and
x+yz=2021
and x, y, and z are integers, and we want to solve for them.
To do that, we should try to manipulate the given equations and try to factor out some terms to be able to solve for integer solutions.
one of the most important things is that 2021-2020 is 1.
🔴I hope you enjoy watching this video.🔴
Don't forget to:
✅ Leave a comment
✅ Subscribe
✅ Hit the like button
✅ Ring the bell
song by Luke Bergs
topics covered in this video:
solving a math olympiad question
solving a system of equations with integer solutions
solving a diophantine equation
2021 math olympiad problem
#solveForIntegers #matholympiad #DiophantineEquation #MathOlympics
Math Olympiad Question | Equation solving | You should learn this trick to pass the exam
A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents
Luxembourg - Math Olympiad Question | You should know this trick
France - Math Olympiad Question | An Algebraic Expression | You should be able to solve this!
Norway Math Olympiad Question | You should be able to solve this!
A Nice Math Olympiad Exponential Equation 3^x = X^9
Math Olympiad Question | You should know how to solve this!!
Math Olympiad 3^m–2^m=65 | Math Olympiad Problems | Algebra
Math Simplification | Can you solve this? nice algebraic equations Math Olympiad | Nice Radical Math
A beautiful international math olympiad problem
The unexpectedly hard windmill question (2011 IMO, Q2)
Thailand | Math Olympiad Question | Nice Algebra Equation
Math Olympiad Question | Nice Algebra Equation | You should know this trick!!
Solving the hardest question of a British Mathematical Olympiad
Germany - Math Olympiad Exponential Problem.
Math Olympiad Question | Indices - Equation Solving | A Must Known Trick
New Zealand - Math olympiad Question
Maths Olympiad | A Tricky Maths Olympiad Questions | Algebra Problem |
Solving IMO 2020 Q2 in 7 Minutes!! | International Mathematical Olympiad 2020 Problem 2
UK - Math Olympiad Question | You should be able to solve this without calculators!!
Solving an IMO Problem in 6 Minutes!! | International Mathematical Olympiad 1979 Problem 1
Chinese IMO team
Solving the Legendary IMO Problem 6 in 8 minutes | International Mathematical Olympiad 1988
Mathematical Olympiad | Solve for a+b | Math Olympiad Preparation
Комментарии
 0:01:54
0:01:54
 0:00:52
0:00:52
 0:02:51
0:02:51
 0:08:40
0:08:40
 0:03:21
0:03:21
 0:02:34
0:02:34
 0:02:24
0:02:24
 0:10:49
0:10:49
 0:08:37
0:08:37
 0:01:00
0:01:00
 0:16:03
0:16:03
 0:01:26
0:01:26
 0:07:26
0:07:26
 0:11:26
0:11:26
 0:04:45
0:04:45
 0:02:44
0:02:44
 0:01:12
0:01:12
 0:08:03
0:08:03
 0:07:35
0:07:35
 0:03:20
0:03:20
 0:06:40
0:06:40
 0:00:34
0:00:34
 0:08:03
0:08:03
 0:08:59
0:08:59