filmov
tv
Number Theory | Modular Inverses: Example

Показать описание
We give an example of calculating inverses modulo n using two separate strategies.
Number Theory | Inverses modulo n
How To Find The Inverse of a Number ( mod n ) - Inverses of Modular Arithmetic - Example
Number Theory | Modular Inverses: Example
Finding the Modular Inverse #numbertheory
Multiplicative Inverse
Extended Euclidean Algorithm and Inverse Modulo Tutorial
What is modular inverse ?
Finding Modular Inverses
What does a ≡ b (mod n) mean? Basic Modular Arithmetic, Congruence
Finding modular inverses by observation
Lecture 9 - Linear Congruences and Modular Inverses
16. Inverse Modulus in Modular Arithmetic
How to find modular multiplicative inverses
Solve a Linear Congruence using Euclid's Algorithm
Multiplicative Inverse Mod n
Number Theory - Modular multiplicative inverse (Arabic)
Modular Inverses, Generators, and Order: Linking Elementary Number Theory and Abstract Algebra
Inverses in Modular Arithmetic
GCD, Bezout, and Modular Inverses | The Extended Euclidean Algorithm
Basics of Modular Arithmetic
Modular Multiplicative Inverse : Modular Arithmetic for Division | CP Course | EP 61
Modulo Operator Examples #Shorts #math #maths #mathematics #computerscience
Solving Modular congruences with Inverses (2/3)
Modular inverse made easy
Комментарии
 0:08:02
0:08:02
 0:10:58
0:10:58
 0:09:41
0:09:41
 0:08:11
0:08:11
 0:10:03
0:10:03
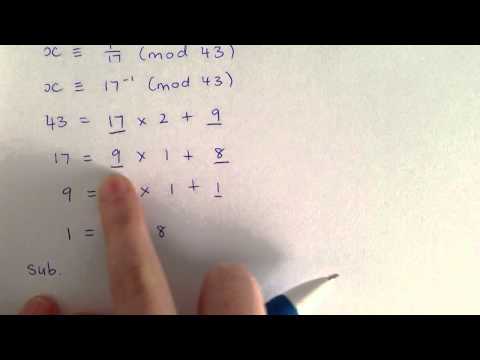 0:06:00
0:06:00
 0:06:25
0:06:25
 0:05:01
0:05:01
 0:05:45
0:05:45
 0:09:46
0:09:46
 0:59:04
0:59:04
 0:02:30
0:02:30
 0:04:20
0:04:20
 0:14:23
0:14:23
 0:17:49
0:17:49
 0:28:01
0:28:01
 0:11:29
0:11:29
 0:30:12
0:30:12
 0:22:21
0:22:21
 0:18:39
0:18:39
 0:16:50
0:16:50
 0:00:30
0:00:30
 0:10:46
0:10:46
 0:04:12
0:04:12