filmov
tv
Finding the Modular Inverse #numbertheory

Показать описание
The modular inverse of a number a modulo n is an integer x such that a * x ≡ 1 (mod n). In other words, it's the number you can multiply by a to get a product that leaves a remainder of 1 when divided by n. This concept is crucial in various fields, including cryptography and number theory.
Q1. What is the modular inverse of 2 modulo 5, that is, 2^(−1) (mod 5)?
Q2. Use the extended Euclidean algorithm to find the modular inverse of 31 modulo 105.
Note: gcd(31, 105) = 1
 0:08:11
0:08:11
 0:10:58
0:10:58
 0:08:02
0:08:02
 0:10:03
0:10:03
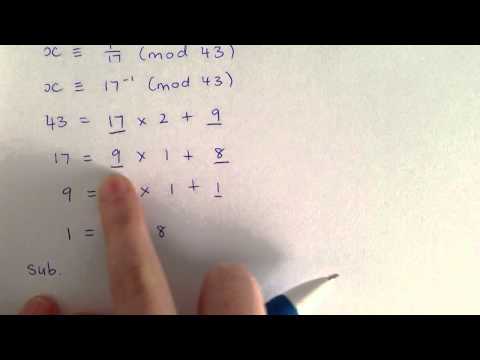 0:06:00
0:06:00
 0:05:01
0:05:01
 0:09:41
0:09:41
 0:09:46
0:09:46
 0:08:38
0:08:38
 0:05:45
0:05:45
 0:03:51
0:03:51
 0:01:33
0:01:33
 0:01:21
0:01:21
 0:04:20
0:04:20
 0:08:22
0:08:22
 0:04:59
0:04:59
 0:06:06
0:06:06
 0:10:57
0:10:57
 0:05:25
0:05:25
 0:06:25
0:06:25
 0:04:12
0:04:12
 0:04:11
0:04:11
 0:16:50
0:16:50
 0:08:05
0:08:05