filmov
tv
Logarithm Fundamentals | Ep. 6 Lockdown live math

Показать описание
Back to the basics with logarithms.
Triangle of power:
Beautiful pictorial summary by @ThuyNganVu:
Thanks to these viewers for their contributions to translations
Hebrew: Omer Tuchfeld
------------------
The live question setup with stats on-screen is powered by Itempool.
Curious about other animations?
Music by Vincent Rubinetti.
Download the music on Bandcamp:
Stream the music on Spotify:
If you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.
------------------
Various social media stuffs:
Triangle of power:
Beautiful pictorial summary by @ThuyNganVu:
Thanks to these viewers for their contributions to translations
Hebrew: Omer Tuchfeld
------------------
The live question setup with stats on-screen is powered by Itempool.
Curious about other animations?
Music by Vincent Rubinetti.
Download the music on Bandcamp:
Stream the music on Spotify:
If you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.
------------------
Various social media stuffs:
Logarithm Fundamentals | Ep. 6 Lockdown live math
What makes the natural log 'natural'? | Ep. 7 Lockdown live math
Introduction to Logarithms (1 of 2: Definition)
How people came up with the natural logarithm and the exponential function #SoME1
LAWS OF LOGARITHM with solved examples.
JAMB Mathematics 2025 EP 8 - Logarithms + Likely Exam Questions & Solutions
Logarithm Simplified - LLL - Episode 1 | Xylem NEET
Triangle of Power
Logarithm Expressions in 3 Minutes - Quick Maths
Trigonometry fundamentals | Ep. 2 Lockdown live math
Logarithm Class 11 | One Shot | JEE Main & Advanced | Arvind Kalia Sir
The essence of calculus
Why use log in IDF ? | Natural Language Processing | EP #6
AZ-900 Episode 21 | Azure Security Groups | Network and Application Security Groups (NSG, ASG)
Logarithm
The Pros and Cons of Log Cabins
I've been playing Ironman Mode... Wrong? IM Progress Ep 6
Back to Basics | EP 7: Critically Reviewing WarcraftLogs | World of Warcraft
Invention Of Computer Programming Language | The Dr. Binocs Show | Best Learning Video for Kids
undefined vs not defined in JS 🤔 | Namaste JavaScript Ep. 6
Common Log | Exponential to Logarithmic Form | Inverse of the Exponential Function Calc 2 Ep. #2
Thanks bhai log(2)
Overhead Shoulder Press - Log Press
Number Raised to Logarithmic Power
Комментарии
 1:34:22
1:34:22
 1:14:54
1:14:54
 0:07:53
0:07:53
 0:33:25
0:33:25
 0:08:09
0:08:09
 0:55:03
0:55:03
 0:03:08
0:03:08
 0:07:42
0:07:42
 0:02:58
0:02:58
 1:13:17
1:13:17
 2:03:14
2:03:14
 0:17:05
0:17:05
 0:20:41
0:20:41
 0:08:43
0:08:43
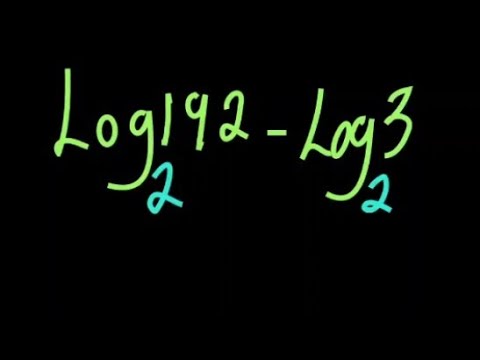 0:01:16
0:01:16
 0:08:46
0:08:46
 0:10:19
0:10:19
 0:11:24
0:11:24
 0:06:37
0:06:37
 0:11:01
0:11:01
 0:06:28
0:06:28
 0:00:16
0:00:16
 0:00:24
0:00:24
 0:00:58
0:00:58