filmov
tv
Triangle of Power
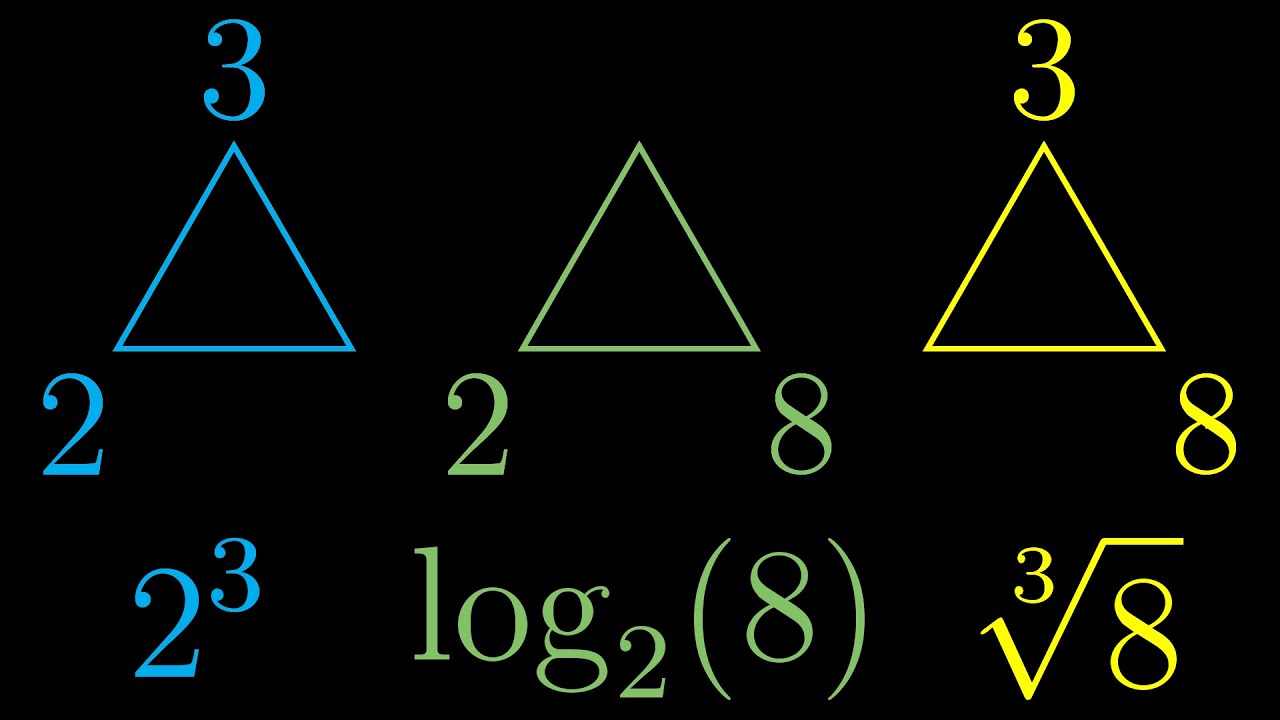
Показать описание
Alternate notation for powers, logs, and roots.
An equally valuable form of support is to simply share some of the videos.
(This is the corrected version of the one I put out a month or so ago, in which my animation for all the inverse operations was incorrect)
An equally valuable form of support is to simply share some of the videos.
(This is the corrected version of the one I put out a month or so ago, in which my animation for all the inverse operations was incorrect)
Triangle of Power
The Triangle Of Power
Response: Triangle of Power
Sadhguru Reveals the Hidden Power of the Triangle | Message From Sadhguru
THE POWER TRIANGLE FOR ELECTRICIANS. What it is, and how to use it.
Power triangle and power factor |Explained
Power Triangle
AC Theory: How to Construct a Power Triangle and the Different Powers in an AC Circuit
50 Min Studio-Style POWER VINYASA YOGA (w/ break for playtime)
Sadhguru Reveals the Hidden Power of the Triangle
Power factor explained | Active Reactive Apparent Power correction
Understanding Power Factor and the Power Triangle | Electrical Engineering Basics.🔔
'The Power of the Triangle'
TRUE Meaning of The Holy Trinity, Triangles, and the Number 3
What is the Triangle of Power? | Worldbuilding Tips for GMs & Writers
Triangle of Power - Concept - 1
The Power of The Triangle - Number 3
The Power Triangle - Learning | Whiteboard Session
44 - Power in AC Circuits 1 | Power Triangle - Apparent, Real and Reactive Power
Why Are Triangles Stronger Than Squares?
Understanding the Power Triangle and Power Factor
How to build everything with the power of the triangle. How to make easy assembly marks.
Expanding Using Pascal's Triangle
Impedance and Power Triangle
Комментарии
 0:07:42
0:07:42
 0:02:27
0:02:27
 0:03:27
0:03:27
 0:04:07
0:04:07
 0:10:56
0:10:56
 0:07:55
0:07:55
 0:04:03
0:04:03
 0:10:58
0:10:58
 0:53:57
0:53:57
 0:04:07
0:04:07
 0:20:39
0:20:39
 0:08:32
0:08:32
 0:01:07
0:01:07
 0:09:46
0:09:46
 0:06:30
0:06:30
 0:04:14
0:04:14
 0:05:56
0:05:56
 0:11:47
0:11:47
 0:16:18
0:16:18
 0:01:18
0:01:18
 0:04:13
0:04:13
 0:04:46
0:04:46
 0:08:23
0:08:23
 0:02:40
0:02:40