Trigonometry fundamentals | Ep. 2 Lockdown live math

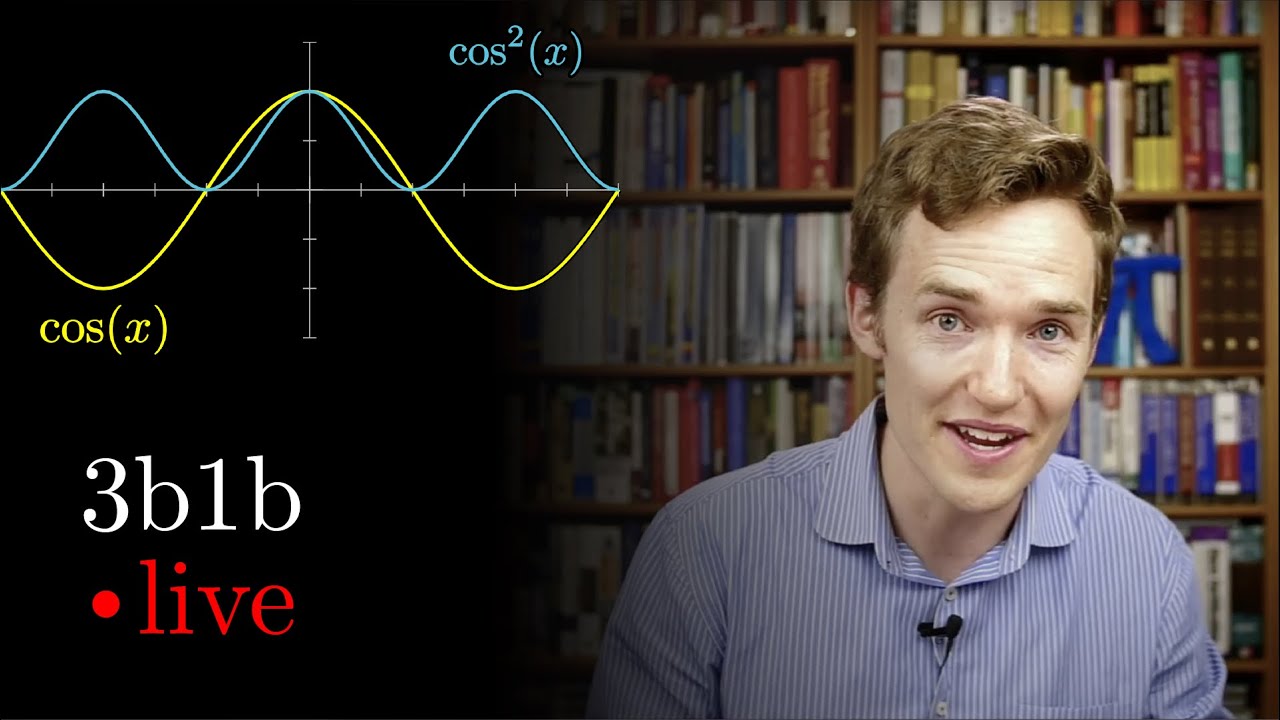
Intro to trig with a lurking mystery about cos(x)^2

Thanks to these viewers for their contributions to translations
Hebrew: Omer Tuchfeld

-----------------

Contents:
Introduction  - 0:00
Q1 Graph of (cos θ)²  - 2:14
Q2 Translations of cos θ to (cos θ)²  - 5:34
Q3 f(2x) = f(x)²  - 10:54
Intro to Trig  - 13:14
Q4 sin(3) & cos(3)  - 16:44
SohCahToa - 20:44
Q5 Leaning Tower  - 22:29
How to Compute Trig Functions?  - 30:59
Q6 sin(π/6)  - 33:34
Q7 cos(π/6)  - 36:19
Q8 Trig of -θ  - 43:34
Computing Trig Functions  - 47:44
Q9 cos(π/12)  - 0:49:54
Adv Trig Functions  - 0:56:44
Q10 Graph of tan(θ)  - 1:00:30
JSON comment  - 1:02:24
“The most exciting part of the lecture” –1:05:34

------------------

The live question setup with stats on-screen is powered by Itempool.

The graphing calculator used here is Desmos.

Curious about other animations?

Music by Vincent Rubinetti.
Download the music on Bandcamp:

Stream the music on Spotify:

If you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.

------------------

Various social media stuffs:

[geoc]

Start of Lecture - 0:00 (Fixed to trimmed video)
Q1 Graph of (cos θ)² - 2:14
Q2 Translations of cos θ to (cos θ)² - 5:34
Q3 f(2x) = f(x)² - 10:54
Intro to Trig - 13:14
Q4 sin(3) & cos(3) - 16:44
SohCahToa - 20:44
Q5 Leaning Tower - 22:29
How to Compute Trig Functions? - 30:59
Q6 sin(π/6) - 33:34
Q7 cos(π/6) - 36:19
Q8 Trig of -θ - 43:34
Computing Trig Functions - 47:44
Q9 cos(π/12) - 0:49:54
Adv Trig Functions - 0:56:44
Q10 Graph of tan(θ) - 1:00:30
JSON comment - 1:02:24

“The most exciting part of the lecture” – Grant 1:05:34

[goofyrice]

When people were voting on 4 options, the most voted bar should have been brown, so there were 3 blue and 1 brown bars.

[xristiano_talimpan]

Youtube's new feauture allows for timestams to be shown in the video progress bar, so a nice idea would be to add timestamps in the description so we wouldn't have to scroll.

[artvandalay]

3b1b: makes a video on high school math topic

Comment section: *grown adults with full time jobs*

[AalapShah]

It's amazing how this livestream has better editing than so many non-live videos. Live quizzes, Q&A, seamless switching between so many screens - all after already delivering top notch content.

[anteconfig]

I've only watched 38 min so far and I'm already thinking that this is exactly how we should be teaching students. Live or not, in class or online. You sir, are a good teacher. You should be like a consultant for some school board of education or something. What the world needs is more teachers who can teach like you.

[ri-ljev]

This man is literally the Bob Ross of math 🤣

[jlpsinde]

Incredible, thank you very much.
I'm a physics teacher, 45, and since 1990 I've never seen such an interesting and imaginative talk about trigonometry!

[Ikantspell]

I wish I was 15 again and could relearn everything with your instruction. These lectures are beautifully crafted, clear and easy to follow.

[pkenon]

Start (he appears on camera) 9:14
12:16 Housekeeping and preliminary question finished
14:00 Question 1
16:10 Answer reveal, 16:36 further explanation
17:40, Question 2
20:10 Answer reveal, 20:40 further explanation
22:02 Pen and paper, (cos(x))^2 = (1+cos(2x))/2
23:02 Question 3
23:48 (Accidental answer reveal)
25:26 "You think it's about triangles, but really it's about circles."
26:09 Sin(x) animation
27:30 Cos(x) animation
28:51 Question 4
30:45 Answer reveal
33:00 Pen and paper, Soh Cah Toa
34:45 Question 5
37:02 Answer reveal and explanation
39:51 Pen and paper, Unit circle
41:50 Radians and degrees connection
43:00 How do you compute these values?
44:12 Special right triangles
45:32 Question 6
46:15 3b1b answers, Do you use pen or pencil?
47:20 Q6 Reveal
48:30 Question 7
49:41 Answer reveal
51:14 Pythagorean theorem connection
54:50 New page, Question 8
57:25 Answer reveal
59:43 Back to cos^2 (x)
1:02:00 Question 9
1:04:25 Answer reveal
1:09:00 Where is tan(x)? Where is cos^2 (x)?
1:11:46 Tangent animation
1:12:30 Final Question
1:14:34 The 'hackerman comment'
1:15:16 Final question, answer reveal
1:16:41 Animation
1:17:45 Back to the tower problem
1:22:00 Fully labeled and explained triangle
1:23:54 Textbook formula connection
1:25:08 Goodbye, Patreon supporter screen

Fin

[sachingiyer]

The tan part was extremely fascinating. Sad that they never teach such stuff at school. Would have had a much better understanding of trig if these things are taught.

Edit: Now also managed to figure out sec and cosec with how you found tan. At last the names make sense. You're a godsend Grant!

[NathanaelKuechenberg]

Compare this with my University lectures and there is no comparison. We need to have this type of fun in the University and have the time to ponder and think instead of rushing at the speed of light and cramming for a test.

[pkmath]

Hey Grant. I very much enjoyed your streaming. As a math professor, trig is always one of the topics where most of the students struggle with the most especially for high school or even college students. What I focused on the most is how to visually make them understand especially the relationship among sin, cosin, and tangent as they can be used and manipulated to figure out csc or others. Your manim seems to be a great way to visually make students understand trig more than any other tools available now. Good job and I very much enjoyed!

[HexerPsy]

Can i just say - im approaching 30, I havent touched these formulas for about 12 years. Much of it I have remembered, much of it is a new approach for me.

The teaching method, the music, the setting, the ease to following this.... OUTSTANDING CONTENT :D

[skilz]

When you got to about the midpoint of the video and started to talk about the Pythagorean Identity of the Trig Functions, I would like to elaborate on this and add to it. We know that the Pythagorean Theorem is: A^2+ B^2 = C^2. Let's keep this in mind.

I will show and prove 4 - 5 different things that most math classes never fully express and these are the following:
* The Pythagorean Theorem and the Equation to a Circle are symbolically similar, also The equation to the Unit Circle centered at the origin is, in fact, the Pythagorean Theorem! It's just that one is in terms of right triangles and the other is in terms of a circle with a radius of 1.
* That there is a direct relationship of the Trigonomic Functions and linear equations in regards to their slopes.
* Without considering the use of limits and applying them, the Tangent Function is, in contrast, the definition of the slope function that is used to define a derivative within Calculus.
* That vector notation is symbolic of both linear and trigonometric calculations. For example ⟨a, b⟩=∥a∥∥b∥cosθ which states that the dot product between two vectors is the product of their magnitudes multiplied by the cosine of the angle between them. So if you know the lengths of two vectors you can find the angle! After you calculate the dot product, then you would have to take the arccos of that value, however, make sure you are using the right system (degrees, radians) to get the correct result you are looking for.
* All of this is rooted in the simplest of all mathematical expressions, not even an equation or a function, just a simple expression, being the very first one we are ever taught: (1+1) and that the operation of adding one to itself satisfies the construction of both the Unit Circle and defines the Pythagorean Theorem. Also, when we turn this into an equation (1+1) = 2 we will see that there is perfect symmetry, reflection, and rotation that is embedded within this.

The comparison of the Pythagorean Theorem and the Equation to a Circle:
The equation to an arbitrary circle is defined by (x – h)^2 + (y – k)^2 = r^2 where (h, k) is the 2D coordinate of the center of the circle.
Let's center this at the origin (0, 0) and refer to the unit circle with a radius of 1. We now end up with: (x-0)^2 + (y-0)^2 + 1^2 = x^2 + y^2 = 1.
Let's compare this to the Pythagorean Theorem. x^2 + y^2 = 1 == A^2 + B^2 + C^2 when C = 1. So for any circle that is centered at the origin, it's equation is the Pythagorean Theorem.

The direct relationship of the Trigonometric Functions and Linear Equations:
We will use the slope-intercept form of a linear equation: y = mx+b. We know that m is defined by rise/run or (y2 - y1)/(x2 - x1) where can use the coordinate points to find the slope. The value of this slope is a proportion of how much change in height over the change in the horizontal. All angles will be relative to the line y = mx+b and the x-axis. In other words, it is the angle that is above the X-axis or the Horizontal axis up to the line itself. Here I mentioned the rate of change. We can take rise/run or (y2-y1)/(x2-x1) and rewrite this as dy/dx. We know that we can make a right triangle from the x-axis up to the line in question. By doing so we can see that the dy is also sin(t) and dx is cos(t). We can see that the slope of the line m is also the tangent of the angle above the horizon to that line. So we can rewrite the slope-intercept form y = mx+b to y = tan(t)x + b or sin(t)/cos(t)x + b. This will lead us to the next section about derivatives!

The Tangent Function and the Derivative: We know that when we have a curve that its slope is not constant. We can take two points on that curve that are relatively close and get a good approximation of its slope near that point, however, the farther the gap the more margin of error this is. This approach is what is referred to as finding the secant slope. If we make smaller and smaller incremental steps where we get closer and closer to that point where the limit of the size of that step approaches 0, we then end up with a line that has the slope of that point which is tangent to that curve at that point. This is seen in the difference quotient in Calculus to find a derivative. f'(x) = lim dx->0 (f(x+dx) - f(x))/dx Which is basically taking the slope form of a line (y2 - y1/(x2-x1) and rewriting it from point notation into function notation with respect to x, changing the difference in points to rate of change by using delta x and delta y, which is still all algebra, and the only part that is Calculus is when you actually apply the limit! So in a sense, we can see a direct relationship and similarity of (f(x+dx) - f(x)) / dx and tan(t). If we substitute tan(t) as sin(t)/cos(t). We can see that cos(t) = dx which is straight forward. However, if we look at f(x+dx) - f(x) it isn't quite obvious but this would be equivalent to sin(t). Where t is the angle above the x-axis and up to the point on the curve whose slope is the tangent of that angle produced by that linear equation.

The vector portion should be self-explanatory as I had already mentioned the most important piece and that is the dot product in relation to the cosine of the angle between those two vectors. Not much more needs to be expressed about this here, but will be referred in the last section.

(...continued in a reply to this post)

[shub]

I am in absolute awe of this lesson. It’s structured so perfectly and I enjoyed every moment of it. Thank you for dedicating yourself to raising the bar of math education. I have no doubt thousands of teachers for years to come will use this and your other lessons as a model to teach this material. And no, I don’t think I’m being hyperbolic here.

[basantachaulagain]

When he explained the tangent part, everything came together. A whole new perspective.

[adrianfernandez]

Grant, thank you for the BEAUTIFUL knowledge you said in the live stream. I’ve never been so intrigued by trigonometry until I saw this. Never really understood how trig worked in circles, the relationship between Pythagora’s theorem and Trig identities. This video has surpassed any trig class I have taken in my life. Thank you 😁

[lewismassie]

After the last one, I went and watched the entire imaginary numbers series by Welch Labs that Grant recommended, and seriously had my mind blown. Highly recommend

[tylern]

This series is a gem. I really hope you can continue this sort of livestream after the covid 19 lockdown has passed, because it is truly a wonderful experience.