filmov
tv
Proof: √3 + √2 is irrational

Показать описание
Proof: √3 + √2 is irrational
Proof: Square Root of 2 is Irrational
A Proof That The Square Root of Two Is Irrational
Prove that root2+root3 is irrational-Real numbers-Class10
Proof that Square Root 2 is Irrational
Prove that 3 + 2√5 is irrational.
Proof that square root of 2 is irrational | Algebra I | Khan Academy
3 + 2 = 4 Proved | How to prove it.
Proof of the difference of Two Cubes | Simplified Algebraic Explanation
The 360-Page Proof That 1+1=2
Prove A Number Irrational in 5 Seconds 🔥 #shorts #ytshorts #maths #class10maths
1 + 1 = 3 Proof | Breaking the rules of mathematics
'Prove' 3 = 0. Can You Spot The Mistake?
Proof that the square root of ANY integer is irrational (besides perfect squares)
Prove that root 2 + root 3 is Irrational
Induction Inequality Proof: 3^n is greater than or equal to 2n + 1
Proof that square root of prime number is irrational | Algebra I | Khan Academy
Prove: Number of Diagonals of a Polygon
The 379 page proof that 1+1=2
Prove that 2 + root 3 is irrational
Crazy math question. Prove that 2=3 🤔. #mathshorts #algebra #education
Prove by induction, Sum of the first n cubes, 1^3+2^3+3^3+...+n^3
If 3n + 2 even, then n even. proof by contradiction
'Prove' 2 = 1 Using Calculus Derivatives - Can You Spot The Mistake?
Комментарии
 0:18:57
0:18:57
 0:04:02
0:04:02
 0:17:22
0:17:22
 0:02:09
0:02:09
 0:06:56
0:06:56
 0:05:12
0:05:12
 0:07:47
0:07:47
 0:10:21
0:10:21
 0:07:17
0:07:17
 0:06:03
0:06:03
 0:00:41
0:00:41
 0:08:25
0:08:25
 0:05:28
0:05:28
 0:06:00
0:06:00
 0:03:51
0:03:51
 0:08:49
0:08:49
 0:07:28
0:07:28
 0:06:12
0:06:12
 0:16:43
0:16:43
 0:04:49
0:04:49
 0:00:50
0:00:50
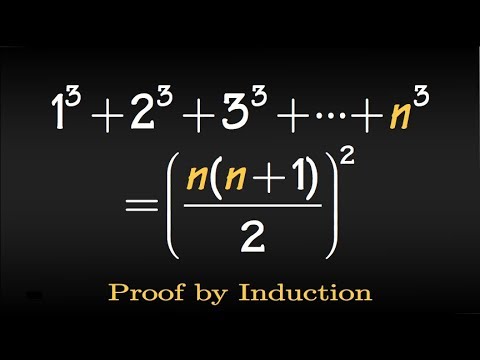 0:09:03
0:09:03
 0:06:03
0:06:03
 0:04:21
0:04:21