filmov
tv
3 + 2 = 4 Proved | How to prove it.

Показать описание
3 + 2 = 4 Proved | How to prove it?
3+2 = 4 can be proved by breaking the ground rules of mathematics. According to mathematics, it is well known to everybody that 3 + 2 = 5. But I have proved through funny math tricks that everything is possible through mathematics if you can break the rules of mathematics. However, as like as other math riddles, this 3 + 2= 4 funny proof is also able to spin anyone's head. The step by step solutions of this 2+3=4 riddles is described here in this amazing math facts video. It is also given the best math proof about how to prove 3+2 = 4. The facts about mathematics are that if someone skips or do a single mistake, the final result would bring a strange output. The same scenario happens in this 2+3=4 fun of mathematics video.
If someone interested to catch that 3 + 2 = 4 kaise hota hai, write it in the comments section and let's discuss there.
------------------------------------------------------------
------------------------------------------------------------
Watch other interesting videos on Matescium
Thanks for watching it.
#Mathtricks #FunnyMath #MathRiddles
3+2 = 4 can be proved by breaking the ground rules of mathematics. According to mathematics, it is well known to everybody that 3 + 2 = 5. But I have proved through funny math tricks that everything is possible through mathematics if you can break the rules of mathematics. However, as like as other math riddles, this 3 + 2= 4 funny proof is also able to spin anyone's head. The step by step solutions of this 2+3=4 riddles is described here in this amazing math facts video. It is also given the best math proof about how to prove 3+2 = 4. The facts about mathematics are that if someone skips or do a single mistake, the final result would bring a strange output. The same scenario happens in this 2+3=4 fun of mathematics video.
If someone interested to catch that 3 + 2 = 4 kaise hota hai, write it in the comments section and let's discuss there.
------------------------------------------------------------
------------------------------------------------------------
Watch other interesting videos on Matescium
Thanks for watching it.
#Mathtricks #FunnyMath #MathRiddles
Комментарии
 0:00:39
0:00:39
 0:10:21
0:10:21
 0:00:23
0:00:23
 0:02:37
0:02:37
 0:00:46
0:00:46
 0:04:20
0:04:20
 0:03:05
0:03:05
 0:10:55
0:10:55
 0:02:43
0:02:43
 0:00:21
0:00:21
 0:01:23
0:01:23
 0:03:00
0:03:00
 0:03:37
0:03:37
 0:00:40
0:00:40
 0:01:09
0:01:09
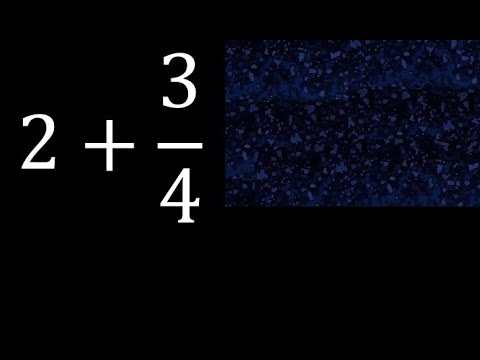 0:00:46
0:00:46
 0:03:35
0:03:35
 0:00:44
0:00:44
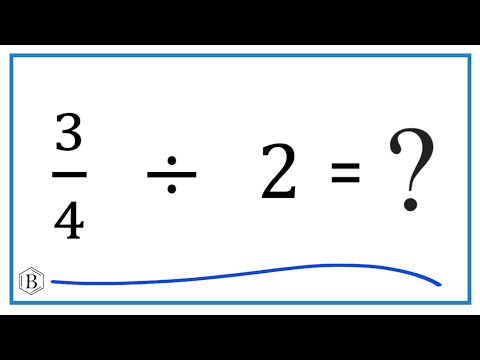 0:01:03
0:01:03
 0:01:26
0:01:26
 0:00:18
0:00:18
 0:12:30
0:12:30
 0:03:55
0:03:55
 0:08:52
0:08:52