Induction Inequality Proof: 3^n is greater than or equal to 2n + 1

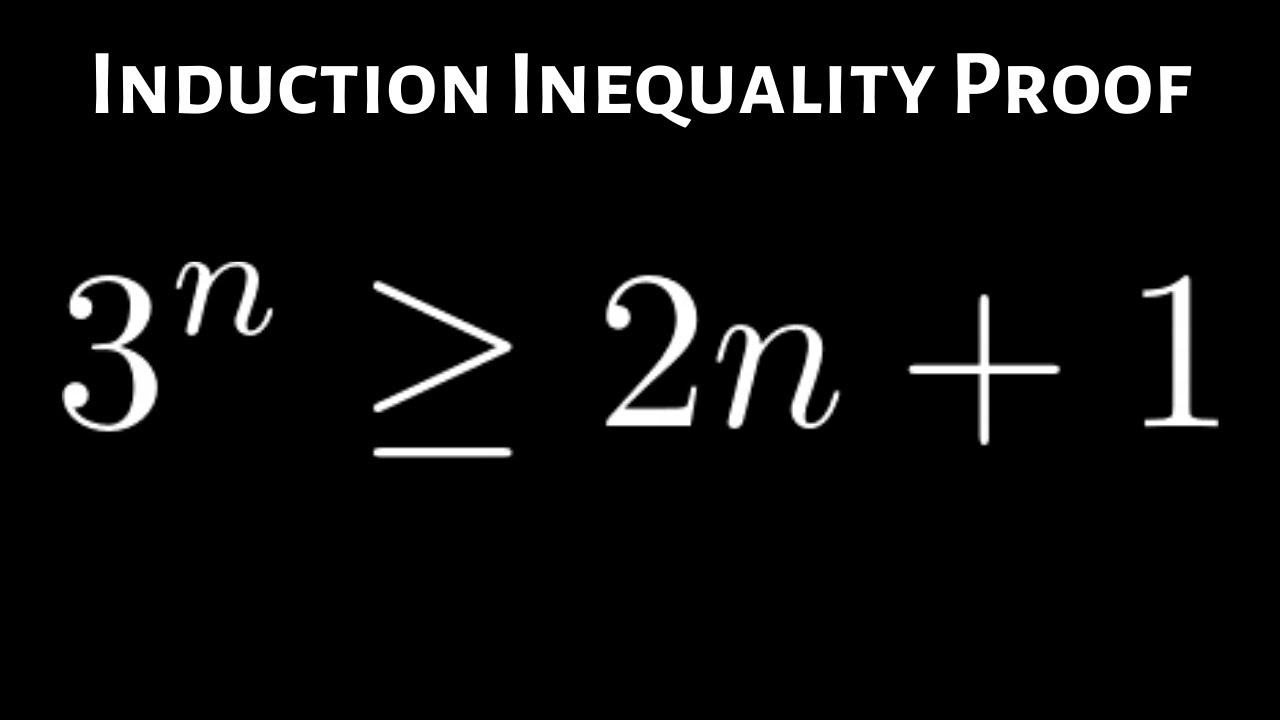
preview_player
Показать описание
Induction Inequality Proof: 3^n is greater than or equal to 2n + 1

If you enjoyed this video please consider liking, sharing, and subscribing.

There are several ways that you can help support my channel:)

************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course

Advanced Calculus Course

Calculus 1 Course

Calculus 2 Course

Calculus 3 Course

Calculus Integration Insanity

Differential Equations Course

College Algebra Course

How to Write Proofs with Sets Course

How to Write Proofs with Functions Course

Statistics with StatCrunch Course

Math Graduate Programs, Applying, Advice, Motivation

Daily Devotionals for Motivation with The Math Sorcerer

Thank you:)
  1. The Math Sorcerer
  2. Induction Inequality Proof: 3^n is greater than or equal to 2n 1
  3. induction proof
  4. inequality
  5. prove
  6. math proof
Рекомендации по теме
Induction Inequality Proof: 0:08:49

Induction Inequality Proof: 3^n is greater than or equal to 2n + 1

Induction with inequalities 0:04:07

Induction with inequalities

Induction Proof: 2^n 0:08:09

Induction Proof: 2^n is greater than n^3 | Discrete Math Exercises

💯 Inequality Proof 0:05:31

💯 Inequality Proof | Prove 3^n is greater than or equal to 2n + 5 by Mathematical Induction

Induction Inequality Proof: 0:10:27

Induction Inequality Proof: 2^n greater than n^3

Example of Proof 0:06:14

Example of Proof by Induction 3: n! less than n^n

Induction: Inequality Proofs 0:14:30

Induction: Inequality Proofs

Inequality Mathematical Induction 0:09:20

Inequality Mathematical Induction Proof: 2^n greater than n^2

Example of Using 0:08:21

Example of Using the Monotonic Sequence Theorem | Calculus 2

#16 proof prove 0:12:47

#16 proof prove induction 3^n less than n+1! inequality induccion matematicas mathgotserved

Principle of Mathematical 0:05:54

Principle of Mathematical Induction Inequality Proof Video

LC HL proof 0:14:11

LC HL proof by induction - inequality proofs

Induction Inequality Proofs 0:07:59

Induction Inequality Proofs (3 of 4: Introducing & transforming the inequality)

00b - Mathematical 0:18:47

00b - Mathematical Induction Inequality

Induction Proofs Involving 0:06:34

Induction Proofs Involving Inequalities.

Induction Inequality Proof 0:10:42

Induction Inequality Proof Example 3: 5^n + 9 less than 6^n

Induction Inequality Proof 0:09:39

Induction Inequality Proof Example 7: 4^n ≥ 1+3n

Mathematical Induction Practice 0:18:08

Mathematical Induction Practice Problems

Unlock the Secrets 0:07:04

Unlock the Secrets of Inequality Proof with Mathematical Induction 🧐🔍

💯 How to 0:09:28

💯 How to Find the Initial Value of an Inequality Proof by Math Induction Explained

Inequality - Proof 0:11:44

Inequality - Proof by induction (Ex 3)

2^n is greater 0:09:22

2^n is greater than n^2. Strategy for Proving Inequalities. [Mathematical Induction]

Mathematical induction with 0:12:53

Mathematical induction with inequality

Induction Divisibility 0:20:35

Induction Divisibility

Комментарии
Автор

Sir, I am literally thankful of this channel and your existence. Thank you!

dccarajay
Автор

Thank you so much Sir . This video is really very helpful for me.

preranabhoi
Автор

Thank the lord this video found me, you saved me hours of pain yet again!

Gizmare
Автор

can you show 3(2k + 2 + 1) by adding values to left side (this should be ok because it's greater than) and then simply say 3(2k + 2 + 1) is greater than 2(k + 1) + 1 because our domain is positive integers and the same equation * 3 is greater than the one that's not

autumnmiloser
Автор

i am so confused as to how and why inequality sign changed mid calculations.

Voyk
Автор

You must used
(1+x)^n>=1+nx
n€IN and x€IR+

maths
Автор

inequality n² ≤ 9 = 0, 1, 2 and 3 I know is -1, -2 and -3 but can someone explain it why or show me step by step

haydeehernandez
Автор

ur thumbnail is different from the proof u do btw lool

jeffreychan
Автор

6:42 the explanation for this makes no sense, you kept the multiplication of 3*1 in 2k+3 but you're free to throw away 3x2k? Where did it go? Why is one okay without the other?

Sellipsis