filmov
tv
Arc Length (Formula)
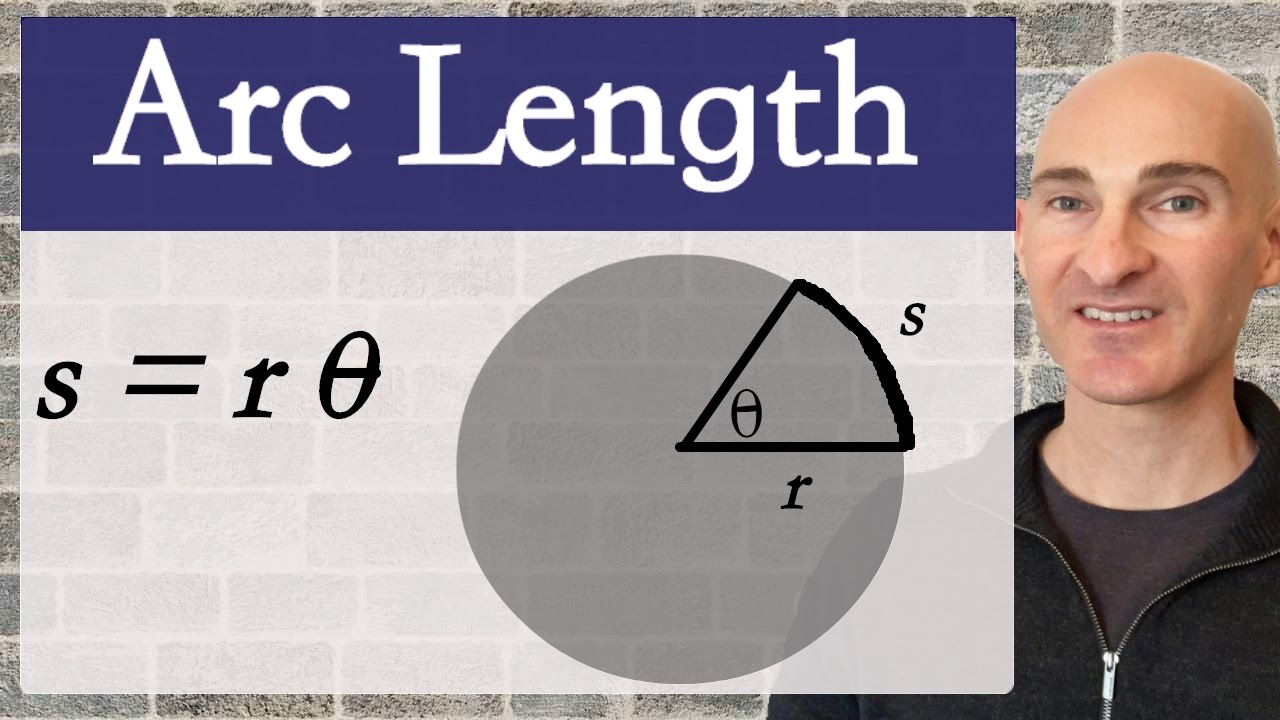
Показать описание
Learn how to find the arc length in a circle using radian angle measures in this free math video tutorial by Mario's Math Tutoring.
0:26 Formula for Finding Arc Length Using Radius and Central Angle in Radians
0:51 Example 1 Find Arc Length Given Radius 10 cm and Central Angle Theta pi/4
1:41 Example 2 Find Central Angle Given Radius 12 cm and Arc Length 8 cm
Related Videos:
Find Arc Length Using Proportions
Finding Area of Sector
Finding Area of Sector Using Proportions
Looking to raise your math score on the ACT and new SAT?
Check out my Huge ACT Math Video Course and my Huge SAT Math Video Course for sale at
For online 1-to-1 tutoring or more information about me see my website at:
* Organized List of My Video Lessons to Help You Raise Your Scores & Pass Your Class. Videos Arranged by Math Subject as well as by Chapter/Topic. (Bookmark the Link Below)
0:26 Formula for Finding Arc Length Using Radius and Central Angle in Radians
0:51 Example 1 Find Arc Length Given Radius 10 cm and Central Angle Theta pi/4
1:41 Example 2 Find Central Angle Given Radius 12 cm and Arc Length 8 cm
Related Videos:
Find Arc Length Using Proportions
Finding Area of Sector
Finding Area of Sector Using Proportions
Looking to raise your math score on the ACT and new SAT?
Check out my Huge ACT Math Video Course and my Huge SAT Math Video Course for sale at
For online 1-to-1 tutoring or more information about me see my website at:
* Organized List of My Video Lessons to Help You Raise Your Scores & Pass Your Class. Videos Arranged by Math Subject as well as by Chapter/Topic. (Bookmark the Link Below)
Arc Length (formula explained)
Arc Length (Formula)
Arc Length Calculus Problems,
Arc Length of a Circle Formula - Sector Area, Examples, Radians, In Terms of Pi, Trigonometry
Arc length intro | Applications of definite integrals | AP Calculus BC | Khan Academy
How to find the arc length of a circle using the formula
I want to show you how to prove the arc length formula
Arclength Formula | Derivation & Ex: Circumference of a Circle
Class 10th Maths Chapter 11 | Areas Related To Circles #4 | 10th Maths By Aakash Sir
Why Students Struggle With Arc Length and How to Help
How long is a curve?? The Arclength Formula in 3D
How do we Find the Length of an Arc? | Circles | Don't Memorise
Arc Length Formula and Sector Area Formula Explained!
Find Arc Length Given Radius and Central Angle (2 Methods)
How to find the perimeter of a sector using arc length formula
GCSE Maths - Area of a Sector and Length of an Arc of a Circle (Circles Part 3) #108
Deriving the Arc Length Formula in Calculus
How to Calculate Arc Length? | Arc Length Formula | Basic Formulas in Geometry | Mathemetics
ARC LENGTH, DEGREE, RADIUS CALCULATION EASY METHOD.
HOW TO FIND ARC LENGTH AND SECTOR AREA OF CIRCLES | GEOMETRY
Arc Length | Calculus 2 Lesson 6 - JK Math
Arc Length & Surface Area examples
Find The Arc Length | Geometry SAT Math Question Practice
Arc Length of Polar Curves
Комментарии
 0:07:57
0:07:57
 0:01:11
0:01:11
 0:30:47
0:30:47
 0:15:57
0:15:57
 0:06:21
0:06:21
 0:02:14
0:02:14
 0:01:25
0:01:25
 0:10:13
0:10:13
 0:43:08
0:43:08
 0:09:57
0:09:57
 0:07:10
0:07:10
 0:03:35
0:03:35
 0:05:35
0:05:35
 0:02:15
0:02:15
 0:02:52
0:02:52
 0:05:39
0:05:39
 0:16:37
0:16:37
 0:00:45
0:00:45
 0:06:03
0:06:03
 0:11:32
0:11:32
 0:27:37
0:27:37
 0:17:35
0:17:35
 0:00:55
0:00:55
 0:10:33
0:10:33