Why Students Struggle With Arc Length and How to Help

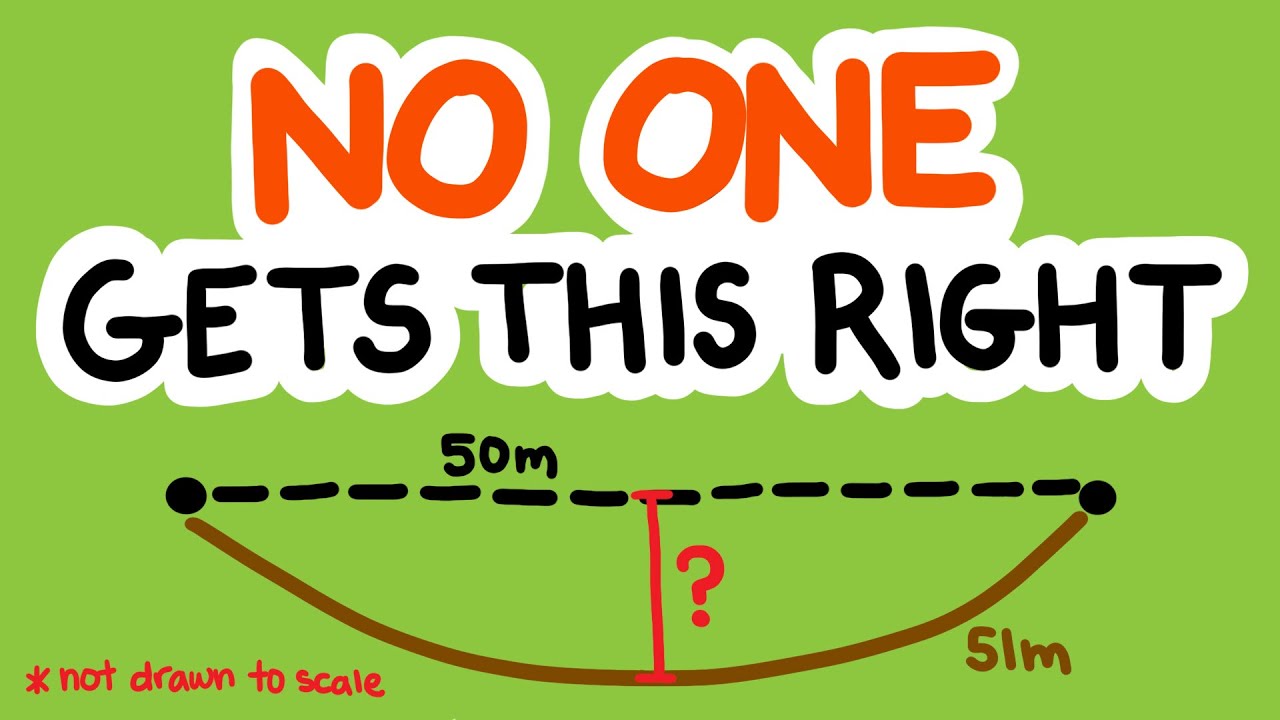
This video dives deep into the topic of finding Arc Length using Integration techniques from Calculus. It answers the question “Why do students struggle to understand the Arc Length Formula?” and goes through a simple break down of how the Arc Length Formula can be derived and then applies this formula to several problems.

Math The World is dedicated to bringing real world math problems into the classroom and answering the age old question “when will I ever use this?”

We use unique algebra context topics, geometry context topics, trigonometry context topics, and calculus context topics. We go beyond context problems and use a technique called mathematical modeling to find solutions to real world questions and real world problems. These videos are great for students who plan to enter technical fields that require real world problem solving, and can be a great resource for teachers looking for ways to bring real world contexts into their classroom.

Created by Doug Corey

Script: Doug Corey and Jennifer Canizales
Audio: Doug Corey
Animation: Jennifer Canizales
Music: Coma Media

© 2023 BYU

[poobob]

4:30 i paused the video and just sat there, wondering why it was never taught like this. That moment you wrote out 1+ m^2, the reason behind the formula "clicked" instantly, far better than the "memorize this it's on the exam" approach my classes took. Excellent job!

[camicus-]

I remember getting a similar problem in class long ago about a rope around the Earth. The question was "If you start with a rope wrapped around the equator of the Earth, how much extra rope would you need to raise it 1 m above the surface?"
Finding out it was only 6.28 m was pretty mind blowing at first

(Just found out this question is such a classic it has its own Wiki page)

[clairecelestin]

Here's a real world example for you- I work in telecommunications, and our data will often run on a fiber optic cable which is strung between poles above ground. If a garbage truck (it's always the garbage trucks!) takes down a fiber line, we can measure the length to the fiber break by sending a light pulse which reflects off of the broken end of the fiber and returns to the source. This time delay (with the speed of light in glass) gives us the length of fiber- this is called Optical Time Domain Reflectometry (OTDR) if you want to read more about it. The time measurements have a precision on the order of tens of nanoseconds, giving break locations with a precision on the order of several meters.
Unfortunately, that measured distance is more like the arc length, but what we really need is the ground position where we need to send the technician with the splice equipment. Since the fiber cables hang in a catenary-like curve, we have to solve this problem every time a break takes place above ground... or get lucky, and hear from the police or a traffic report the intersection where someone has crashed and downed a pole.

[JushuaAbraham-sjxl]

For Q 1 Simple pythagorean formula 5.02 meters. For Q 2 I think it involves catenary calculations

[DaveScottAggie]

Ships have a piece of small rope called a "tattle tale" secured to 2 points on a mooring line. When there is no tension on the mooring line, the tattle tale has a lot of slack in it. As the mooring line stretches, the 2 points move apart and the tattle tale slack is removed. This way, the ship's crew can tell when there is too much strain on the mooring line. The length of the tattle tale and how far apart to secure the ends depends on the specifcations of the mooring line.

[correacarlos]

People like you that knows how to explain maths well, they deserve a place in Heaven. It is always a strugle for me to understand a book math, but then I see videos like yours and it makes everthing so easy.

[PaulMurrayCanberra]

The large amount of horizontal motion needed to take up a tiny bit of slack on the rope also relates to the mechanical advantage that pulling the rope horizontally has on the tension of the rope, how taut rope needs to be to not deflect by that much.

[theskullcrack]

Math was just numbers to me, but after coming across your channel. I see the beauty in it. The art. Every video you've posted has been blowing my mind.

[francescopayan]

professors never seem to explain why any of this is possible. This video makes it incredibly straight forward to understand why

[thegreatbambino]

I dont understand why we assumed the rope makes a parabola. I always thought a uniform density line used catenaey shapesninvolving e^x and e^-x terms

[BigDBrian]

for Q1 I actually guessed 5m. I didn't expect to be so close, but I knew it had to be much bigger than the difference in length. I'd always been surprised by the 5-12-13 Pythagorean triangle which shows that a tiny difference in length between two lines creates a big distance between them at an angle, so I remembered it well.

[dneary]

The athletics example about slack reminded me of the high jump - with a relatively stiff bar, there is still over an inch in height difference at the stanchions and in the middle of the high jump.

[Mr.Not_Sure]

It should be actually quite intuitive for anyone who has been playing with stretched string or rope. It's so easy to make large sag even if string is really tightly stretched. If you think about it for a minute, you'd realize that according to Hooke law, the elongation of the string is small, as well as the applied force.

[adventureboy]

"The simplist way is to ask your friend"
"Hey!! How much did you fall off!!"
"Four point
"Approximately 3 seconds"

[msrjbsr]

I don’t know who you are but you are surely one of the best teachers for the modern generation.

[LilBurntCrust]

I just used Heron’s formula after summing 50, plus 2 times 25, plus 1 and used the base of 50m for the lower part of the triangle and the area I got of approximately 125.6m for a 5.02m drop of your friend when you add 1 extra meter of rope.

[JayJay-lyer]

Thank you Professor Math The World, this will do me good justice.

[Pocketfarmer]

I work on sea going tugboats. We tow barges with a cable. Knowing the sag in the cable is important so it doesn’t touch the bottom. We call it shining the wire. The company policy is add 10 feet of depth for ever layer off the drum. The difficulties arise because every layer is a different diameter, every drum is a different size, and the hight of the barge is always different. The cables themselves are usually 1500 feet long, but you never use the last layer on the drum because that is how it holds on. The diameter of the cable is mostly 1 31/32”. The math is daunting. We rely on experience.

[ctheworld]

As an amateur in sewing and pattern design, this has caused issues for me. A 1mm discrepancy in a 30cm seam can result in a 1cm arc! That's why I think half the battle is cutting fabric pieces as accurately as possible.

[alirezaakhavi]

really amazing, explanation, animation and story thank you very much! subbed :)