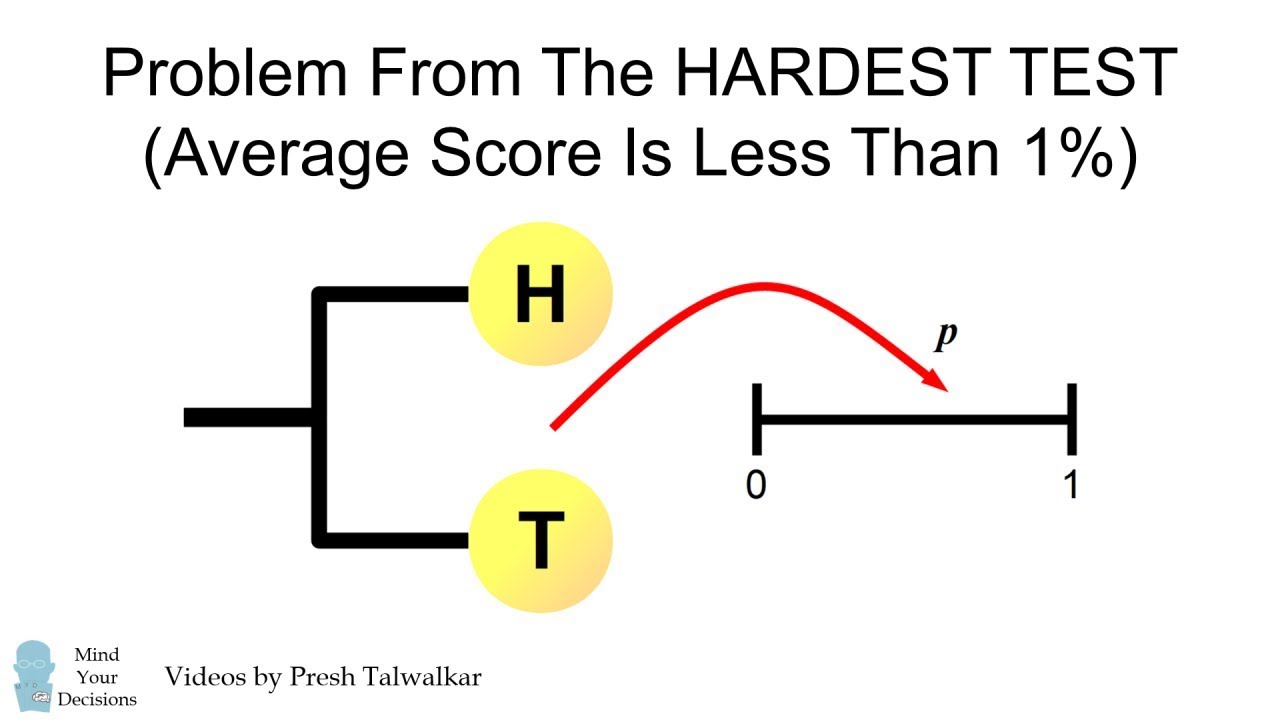
Problem From The Hardest Test - Use A Coin To Simulate Any Probability

How can you simulate any probability from a fair coin? What if you had an unfair coin? This is a great problem from the the Putnam Exam, which has legendary difficulty: the average (median) score is usually 1 out of a possible 120 points. No calculators allowed though, and you have to prove everything very carefully.

My blog post for this video

Thanks to all patrons! Special thanks to:
Kyle
Shrihari Puranik

Sources
1989 Putnam exam, problem A-4

Sorta Insightful

Not really blogging

Janko Gravner's course Math 189 problem set 11

Connect on social media. I update each site when I have a new video or blog post, so you can follow me on whichever method is most convenient for you.

My Books

[asdno]

Can't even understand the question.

[ronaldleemhuis]

Interesting solutions! However, my immediate reaction to the question was to disregard heads or tails on the coin toss and rather look at its rotational position with regard to a reference line. The deviation can be up to 2*pi radians. Just partition the angle in the desired proportion to yield the right probability.

[ok-jkgy]

I Was Trying To Flip A Coin, But...




This One Crazy Math Problem Is Kicking My Ass!

[bestredditstories]

When your life sucks so badly that you have to play a coin-flipping game.

[johnhsieh]

There are some awesome probability concepts in the binary part, loved this puzzle.
I just bought your 2nd puzzles book as well, keep up the good work man

[vicr]

"any rational or irrational number between 0 and 1"
So in other words, any real number between 0 and 1? :)

[hallowurm]

That was a stunningly beautiful solution at the end

[ArthurDgn]

Both solutions don't satisfy the "equal exactly p" in case of irrational numbers (because rely on rational approximations).

[panescudumitru]

"hey this is pressure locker" -auto captions

[nealcarpenter]

Your videos are nearly always worthwhile, but this one was brilliant. I was able to do the 1st part for rational p, but gave up on irrational p; I didn't even try the 'biased coin' problem. Then your explanations were simple and clear. For some; 10 kinds of people - those who understand binary & those who don't.
Now I can give my middle school kids a problem where they can show that they're smarter than I am! They'll love the opportunity and some will work their tails off on it. Thanks.

[BigDBrian]

Isn't just flipping a coin and calling heads or tails already a solution?
p=0.5 = P(heads)
1-p=0.5 = P(tails)

I suppose that's trivial and the real question is to seek a general solution for all rational/irrational numbers between 0 and 1... huh.

[-sideddice]

You could also throw the coin on a sheet of paper with an area of 1. You draw a shape with an area of p and if the coin falls in the shape, then you win, not depending on which face it falls on.

[jean-francoisbouzereau]

The rules say that the game must end in a finite number of flips, but the solution includes the possibility "start over", which do not guarantee this.

[Mephistahpheles]

I've watched a bunch of these. They can be amusing, interesting, this one....

This solution is awesome.

[MumboJ]

Method 2 is simply the Base2 version of a standard D&D tactic:
Using multiple d10s to represent individual digits of a number, roll under the probability.

Most commonly limited to whole percentages, it can easily be extended to any level of precision by rolling further d10s for additional digits as needed.

My proposed solution was attempting to convert coin flips into d10s, but your solution of expressing the probabilities in Base2 seems far easier. :)

[avinashthakur]

If p = 1/3, We need infinite flips because binary representation of 1/3 has infinite digits.
How's this checked ?

[quinnencrawford]

p = 0.5
flip the coin once
there ya have it

[adrienturmo]

But technicaly the binary method doesnt garanty that the game finishes in a finite number of coin toss.

[clementdato]

Just to answer the question about probability = 1. Probability = 1 does not mean that it happens for all cases.
It means that among all the possible cases, the probability - that we will end up in cases where the number of coin flips is finite - is 1.
In the answer of the video, there are cases where we never get a head. But the probability that we end up in these cases is zero.

[dmitrii.zyrianov]

Your two last videos are much better than videos like "many adults are stumped by this riddle". Please keep going this way!