filmov
tv
The Easiest Problem on the Hardest Test

Показать описание
This Putnam Series was given on the Putnam exam in 1997 (Problem A1). Let's figure out a way to deal with this Putnam problem!
For those that don't know, the Putnam math competition features some super interesting and challenging problems!
🙏Support me by becoming a channel member!
Disclaimer: This video is for entertainment purposes only and should not be considered academic. Though all information is provided in good faith, no warranty of any kind, expressed or implied, is made with regards to the accuracy, validity, reliability, consistency, adequacy, or completeness of this information.
Putnam 1997 A1
Putnam Exam 1997 A1
#math #brithemathguy #putnam
For those that don't know, the Putnam math competition features some super interesting and challenging problems!
🙏Support me by becoming a channel member!
Disclaimer: This video is for entertainment purposes only and should not be considered academic. Though all information is provided in good faith, no warranty of any kind, expressed or implied, is made with regards to the accuracy, validity, reliability, consistency, adequacy, or completeness of this information.
Putnam 1997 A1
Putnam Exam 1997 A1
#math #brithemathguy #putnam
The Easiest Problem Everyone Gets Wrong
The Easiest Problem on the Hardest Test
The Easiest Problem on the Hardest Test [2017 Putnam Competition A1]
the trolley problem is easy, actually
Is This THE EASIEST Problem On THE HARDEST Test?
Every Unsolved Math problem that sounds Easy
Every Unsolved Geometry Problem that Sounds Easy
The EASIEST Math Olympiad Problem from 1985
Nightfall Problem? 5 Easy Tips to Stop It Naturally! #fitnessgrow #sportfeed #helthtips #nightfall
This Problem Is Very Easy to Fix 🤯 #shorts
Time is the easiest problem to solve - Alex Hormozi
Easy Way to Solve this Problem 🤯
One of the Easiest IMO problems | International Mathematical Olympiad 1964 Problem 1
A math olympiad problem that looks complicated, but it's easy to solve
I can't believe this is an easy problem
This Problem is Actually Really Easy To Fix 🟥🟩🟧 #howtosolve #rubikscube #cubastic #cubing
Easy SAT Math Problem
The Easiest Putnam Problem ever | Putnam B1 1988
The easiest problem on IMO training camp
This Problem is Actually Really Easy To Fix
Not your problem-Easy tutorial 🔥#dance #dancechallenge #trending #tutorial #subscribe #like #shorts...
How Might We Questions - The EASIEST Problem Solving Exercise EVER (Design Thinking Method)
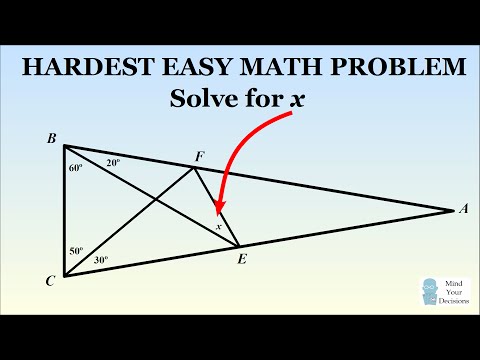
How To Solve The Hardest Easy Geometry Problem
“The immortal snail problem is easy” (the beginning of the saga)
Комментарии
 0:15:04
0:15:04
 0:04:27
0:04:27
 0:13:18
0:13:18
 0:07:00
0:07:00
 0:02:28
0:02:28
 0:12:54
0:12:54
 0:11:37
0:11:37
 0:09:10
0:09:10
 0:03:00
0:03:00
 0:00:30
0:00:30
 0:00:14
0:00:14
 0:00:20
0:00:20
 0:02:05
0:02:05
 0:10:23
0:10:23
 0:00:59
0:00:59
 0:00:17
0:00:17
 0:00:35
0:00:35
 0:06:01
0:06:01
 0:04:24
0:04:24
 0:00:52
0:00:52
 0:00:15
0:00:15
 0:06:49
0:06:49
 0:08:05
0:08:05
 0:00:17
0:00:17