filmov
tv
Correlation Matrix; Test For Significance; Identity Matrix; Significant Relationship
Показать описание
In this video we take a look at how to test a correlation matrix for significance, that is, whether the correlations among the variables are significant or not taken as a whole.
(Remember to click the "Subscribe" button!)
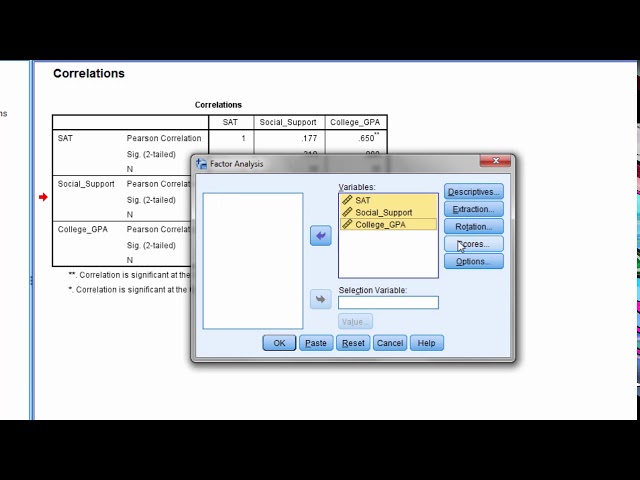
Video Transcript: In this video I'd like to show you how to test a correlation matrix to see whether it's significant. So here I have three variables, SAT social support, and college GPA. And I calculated the correlation matrix in another video, and I saw that two of the bivariate correlations were significant, college GPA with SAT, right here, and college GPA with social support, but that social support and SAT was not significant. Now on a bivariate level, which is what we just looked at, two variables at a time, we saw that two were significant and one was not. But I can also test this entire matrix as it's called at a single point in time to see whether, overall, is this entire matrix significantly different from a matrix in which these values would all be 0 and you have 1s on this main diagonal, which is also known as an identity matrix. And there are applications where we might want to do this, such as in factor analysis as well as in other multivariate procedures, where we want to know before we begin the analysis are the variables significantly correlated in the whole system of variables. Are they significant, or are they just within sampling era of zero. So that's what we're doing when we test this correlation matrix against the identity matrix. So do that we want to go to Analyze and then go to Dimension Reduction and then select Factor. And then here I'm going to move my three variables over to the variables box, and then go ahead and select Descriptives. And here what I want to select is KMO and Bartlett's test of sphericity. Click Continue. And then click OK. Now in our output I'm going to delete these last three tables, as they aren't relevant to what we're looking at here. But notice this table here, KMO and Bartlett's test. What we want to look at is this p-value right here. And if this p-value is less than .05, if we're using an alpha .05, then that means that this matrix is significantly different from zero. In other words, we're testing this matrix, with these observed correlations here, against a matrix of ones on this main diagonal, and zeros in all other places. So, essentially, no correlation here, no correlation here, no correlation here, or if you're looking at the mirror image, this side which is the exact same as this, it's just the mirror image of it, no correlations here, whichever side you prefer to look at. So this test here tests whether this matrix, once again, is significantly different from a matrix with ones and zeros everywhere else, which means no correlations. And that's called an identity matrix, ones on the main diagonal 0 everywhere else. And if we look at this note here we click on Bartlett's test, right-click the mouse and then go to What's this? Let's look at this first line here. Tests the null hypothesis that the correlation matrix is an identity matrix. This is testing whether this matrix is significantly different from matrix with ones on the main diagonal, and zeros everywhere else. So because this result was significant, and quite significant, .000025, this gives us confidence that these variables in this matrix, if we look at the matrix as a whole, not on a bivariate level, but overall, that these variables are significantly correlated, they're significantly different than an identity matrix. Now that doesn't tell us or ensure that every single variable is correlated with every other variable, as we saw right here SAT and social support is not significant, but it does give us confidence that there are significant relationships overall in our matrix when taken as whole. And therefore we can go ahead and do further analyses like a factor analysis or some other multivariate analysis, where it depends on that are variables are correlated to begin with, at a multivariate level. OK that's it. Thanks for watching.
(Remember to click the "Subscribe" button!)
Video Transcript: In this video I'd like to show you how to test a correlation matrix to see whether it's significant. So here I have three variables, SAT social support, and college GPA. And I calculated the correlation matrix in another video, and I saw that two of the bivariate correlations were significant, college GPA with SAT, right here, and college GPA with social support, but that social support and SAT was not significant. Now on a bivariate level, which is what we just looked at, two variables at a time, we saw that two were significant and one was not. But I can also test this entire matrix as it's called at a single point in time to see whether, overall, is this entire matrix significantly different from a matrix in which these values would all be 0 and you have 1s on this main diagonal, which is also known as an identity matrix. And there are applications where we might want to do this, such as in factor analysis as well as in other multivariate procedures, where we want to know before we begin the analysis are the variables significantly correlated in the whole system of variables. Are they significant, or are they just within sampling era of zero. So that's what we're doing when we test this correlation matrix against the identity matrix. So do that we want to go to Analyze and then go to Dimension Reduction and then select Factor. And then here I'm going to move my three variables over to the variables box, and then go ahead and select Descriptives. And here what I want to select is KMO and Bartlett's test of sphericity. Click Continue. And then click OK. Now in our output I'm going to delete these last three tables, as they aren't relevant to what we're looking at here. But notice this table here, KMO and Bartlett's test. What we want to look at is this p-value right here. And if this p-value is less than .05, if we're using an alpha .05, then that means that this matrix is significantly different from zero. In other words, we're testing this matrix, with these observed correlations here, against a matrix of ones on this main diagonal, and zeros in all other places. So, essentially, no correlation here, no correlation here, no correlation here, or if you're looking at the mirror image, this side which is the exact same as this, it's just the mirror image of it, no correlations here, whichever side you prefer to look at. So this test here tests whether this matrix, once again, is significantly different from a matrix with ones and zeros everywhere else, which means no correlations. And that's called an identity matrix, ones on the main diagonal 0 everywhere else. And if we look at this note here we click on Bartlett's test, right-click the mouse and then go to What's this? Let's look at this first line here. Tests the null hypothesis that the correlation matrix is an identity matrix. This is testing whether this matrix is significantly different from matrix with ones on the main diagonal, and zeros everywhere else. So because this result was significant, and quite significant, .000025, this gives us confidence that these variables in this matrix, if we look at the matrix as a whole, not on a bivariate level, but overall, that these variables are significantly correlated, they're significantly different than an identity matrix. Now that doesn't tell us or ensure that every single variable is correlated with every other variable, as we saw right here SAT and social support is not significant, but it does give us confidence that there are significant relationships overall in our matrix when taken as whole. And therefore we can go ahead and do further analyses like a factor analysis or some other multivariate analysis, where it depends on that are variables are correlated to begin with, at a multivariate level. OK that's it. Thanks for watching.
Комментарии























