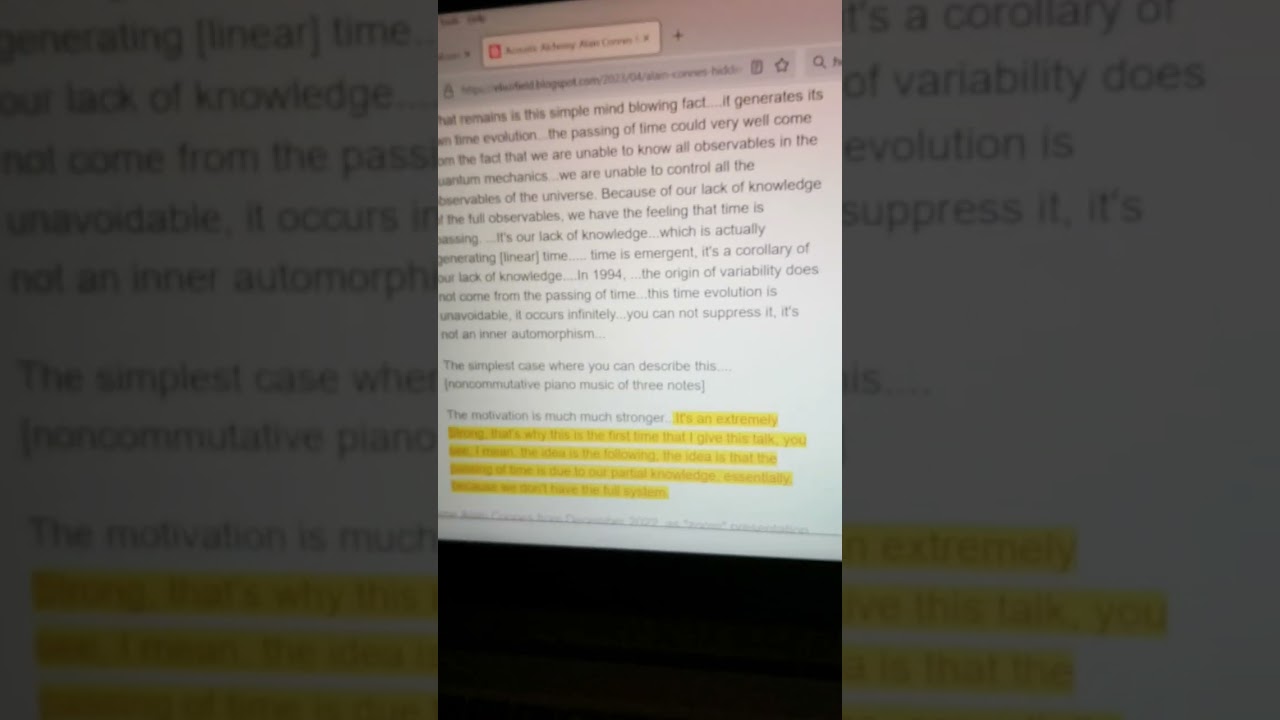
Alain Connes: the passing of time is due to our partial knowledge b/c we don't have the full system

Alain Connes: "The motivation is much much stronger...It's an extremely Strong, that's why this is the first time that I give this talk, you see, I mean, the idea is the following, the idea is that the passing of time is due to our partial knowledge, essentially, because we don't have the full system." 41 minutes into his 2015 talk to physicists
Alain Connes - Temps et aléa du quantique

And emails to me from Physics Professor Basil J. Hiley (who cites Kauffman): Wed, Feb 23, 2022, 4:19 AM (from Professor Basil J. Hiley)

“...However non
-commutativity is deeply ingrained in quantum phenomena and is
not, in my opinion, “only mathematics”. The early pioneers of QM, such as
Heisenberg, Born, Jordan, Dirac and others showed this feature of non-
commutativity in great detail. It was Schrödinger’s work that led to the
development of a tremendously successful algorithm based on the notion of a wave function which was formalised into the bras and kets that we have got very very used to manipulating. However by identifying the wave function with the 'state of
a system’ we have been left with the unsolved ‘problem', the collapse of the wave
function. After one hundred years of effort we have been unable to 'solve this
problem’. In the last few years I have come to the conclusion that this is
unsolvable simply because it is the wrong question as it is based on treating an algorithm rather than a description of an unfolding process.

The availability of the ‘algorithm’ which was easy to manipulate and lead to
experimental verification should be contrasted with
the difficulty in understanding non-commutativity, both mathematically and conceptuality
. Furthermore it was very difficult to apply it to physical
problems. Then there follows an attempt to make the formalism into an
ontology
and the result is a plague of interpretations.

It is a very different approach which is based on an exploration of non-commutative geometry, in the same spirit of Alain Connes but using more physical intuition. It is a long story but I have a lecture online at emmy network which may help. My lecture
is Lecture 2 immediately after Roger Penrose’s lecture in the series ‘Mind and Matter’. My lecture was about 'Matter’ not ‘Mind'!

Mon, Aug 29, 2022, 6:27 AM

“Dear Drew,

In my approach there is no need to refer to any wave function. Each individual process is described by the non-commutative elements of the phase-space algebra itself.
Classical physics uses a commutative phase-space algebra
. Classical physics has the Poisson brackets as a vital part of the description. What we have to understand is how that [Poisson] bracket
emerges from the non-commutative structure
. Now the non-commutative algebra contains two types of bracket, a commutator or Lie bracket (or Lie product to give it its proper mathematical name) and an anti-commutator or Baker bracket (known as the Jordan product). The Lie bracket becomes the Poisson bracket as we go to the classical limit, while the Jordan product becomes the normal inner product. In symbols (AB + BA)/2 is greater than AB. The Jordan product is the most neglected product in the whole discussion of the foundations of quantum mechanics.
This is not a 'cheat answer’. It's what you have to understand if you
really
want to understand the relation between quantum and classical physics. The clearest discussion of this issue is in the paper I have attached.

I hope you find it helpful.

Basil Hiley.

Mon, Aug 29, 2022,

“It is the spin that led me to the idea of no ‘waves’.

Of course you have to explore the algebraic way and see if it makes more sense. I do and to me it fits more naturally into the mathematical scheme I am developing. By the way it is not just me
.But there is much more interesting ideas being developed i.e.
Alan Connes “Noncommutative Geometry.
"

Basil Hiley.

Sun, Sep 25, 2022, 11:20 AM

“Dear Drew,

My silence is not because I did not appreciate the Connes lecture and your summary of the highlights. It is
really deep stuff which moves us well away from the way physics is normally presented
.
It shows how the
non-commutative geometry produces discrete energy level structure

[voidisyinyangvoidisyinyang]

This "one frequency" or "tone" controlling us is actually the concept of irrational magnitude as symmetric space to define time - it was created by Philolaus flipping his Lyre around - what I call the "Liar of the Lyre" thereby hiding the truth of noncommutativity. The "one" is not a materialistic wavelength but rather a formless awareness of protoconsciousness from listening to the source of sound as complementary opposites - the future and past overlapping. This is explained by ONLY the top math professor, Fields Medal Math Professor Alain Connes calls this secret, "Two, Three, Infinity" - because the Perfect Fifth as the undertone is C to F as 2/3 while 3/2 is C to G as the overtone. The Perfect Fourth is NEVER a natural overtone of the fundamental tonic since 3 in the denominator is not a natural same pitch harmonic of the root tonic as an octave. This means the Perfect fourth creates a NEW "one" as the undertone that is noncommutative Perfect fifth as a time-reversed negative frequency signal with the TRUE "fundamental tone" as the Ghost Tonic that is superluminal antigravity sound. thanks - see my channel for more details - free research: books and papers, training manuals, etc. thanks

[voidisyinyangvoidisyinyang]

Nazis in South America - yes the U.S. brought in 1600 Nazi scientists via Operation Paperclip but the CIA Nazi network brought thousands more into South America. The "Cocaine Coup" of Bolivia included Klaus Barbie, the "butcher" of France. The Argentinian Nazi torturers trained Operation Condor for Central American genocide using US "field radios" to electrocute genitals. "Ten days after the 1973 coup against the Popular Unity (UP) government of President Salvador Allende, the military opened the Río Chico concentration camp on Dawson Island, located in the Strait of Magellan, near the southern tip of Chile. The island had served as an extermination camp by a Catholic order between 1891 and 1911 to confine the Selk’nam and Kawésqar peoples, who died due to overcrowding, the spread of disease, and the cold.
The coup regime sent 38 officials of the UP government to the Compañía de Ingenieros del Cuerpo de Infantería Marina (COMPINGIM) naval base and then to the Río Chico camp. It also sent hundreds of political prisoners to Punta Arenas, near Dawson Island. The officials were interrogated, tortured, and forced to work on the island’s infrastructure. The Río Chico camp was dismantled in 1974."
This is not ancient history. Good researchers on this: Peter Levenda, Professor Chris Simpson, Colin Ross, and John Loftus. Also Antony Sutton. thanks. The biography of Allen Dulles by David Talbot (Devil's Chessboard) and H.P. Albarelli - other excellent sources. Noam Chomsky's book "Political Economy of Human Rights" was first censored and had to be republished by a small nonprofit press. Counter-Revolutionary Violence: Bloodbaths in Fact & Propaganda is a 1973 book... (Wiki): Chomsky and Herman argued that the American treatment of bloodbaths was related to their political utility, regardless of the objective facts of such murders. Benign bloodbaths were those in which the United States' political establishment had little strategic interest and were often committed by friendly nations (and the United States regularly supplied the regimes committing the murders), constructive bloodbaths had strongly favorable results for American (primarily corporate) interests, nefarious bloodbaths were conducted by official enemies, and mythical bloodbaths either never happened or were minor events inflated into legendary status by government and media exaggeration.
Publishing history

The work was published by Warner Modular Publications, a subsidiary of Warner Communications in 1973.[1] The head of Warner Publishing wanted to stop the publication of the book, and Warner Modular was shut down as a result.

Warner Modular initially agreed to print 20, 000 copies of the book. Warner Modular's publisher, Claude McCaleb, had spent his career publishing books for universities, and CRV was planned as part of a series of works that studied American institutions, which McCaleb believed would be timely after the Watergate scandal. Warner Modular had prepared ads to run in various periodicals that promoted CRV, in anticipation of an upcoming convention of the American Sociological Association in New York City. According to McCaleb, in an affidavit to Chomsky and Herman quoted in Ben Bagdikian's The Media Monopoly, on August 27, 1973, the chief of book operations at Warner Communications, William Sarnoff, nephew of David Sarnoff, saw the ads come across his desk and called McCaleb's office in Andover, Massachusetts and Sarnoff asked if CRV would be another Pentagon Papers that would embarrass Warner. McCaleb replied that it was not a document leak, but was an analysis of public material by two established academics. Two hours later, Sarnoff called again and asked McCaleb to fly that night and bring an advance copy of the book to his office in New York City.[2][3] In the morning McCaleb dropped off the book at Sarnoff's office and then went to the booth at the American Sociological Association's conference, awaiting the advance copies of CRV that were just coming off of the presses. Within a few hours, Sarnoff asked McCaleb to come back to his office.[4] McCaleb is quoted as saying:

Sarnoff immediately launched into a violent verbal attack on me for having published CRV saying, among other things, that it was a pack of lies, a scurrilous attack on respected Americans, undocumented, a publication unworthy of a serious publisher.

McCaleb reminded Sarnoff of the arrangement that they had when McCaleb was hired: he and his staff were given discretion to select what to publish, and that their sales levels would measure their success. Sarnoff dismissed McCaleb's argument by stating that the arrangement did not cover works that were "worthless and full of lies." Sarnoff complained that too many of Warner Modular's works were written by left-wing writers. McCaleb replied that conservative writers were also represented, and that Warner Modular had planned to publish works by Milton Friedman and Friedrich Hayek.

Sarnoff then canceled the ads for CRV, ordered the destruction of the first printing of CRV, as well as the Warner Modular catalog that listed them, and announced that he would not release one copy of CRV to anybody. When McCaleb replied that such an outrageous move would shatter Warner Modular's staff and shock the publishing world, Sarnoff replied that he did not "give a damn what I, my staff, the authors, or the academic community thought and ended by saying that we should destroy the entire inventory of CRV".[5][2]

Warner Publishing decided to shut down Warner Modular before CRV could be published. The print run was not initially destroyed because of contractual obligations, but the book was passed on to MSS Information Corporation for promotion and distribution after Warner Publishing shut down Warner Modular.[1][6] However, MSS engaged in no promotion, as it was not a commercial publishing company and had no distribution facilities. Only 500 copies of the 20, 000-copy printing survived. Radical America obtained and distributed some copies, because its staff already knew of CRV's existence.[6] According to Chomsky, the rest were "pulped, " not burned.

[voidisyinyangvoidisyinyang]

This new Connes talk has a French title but the talk is in English.

[voidisyinyangvoidisyinyang]

Thanks again and hope your Chopin is going well. haha.
drew hempel

[voidisyinyangvoidisyinyang]

0 seconds ago
Olivier Costa de Beauregard's book "Time: A physical magnitude" argues it's all based on precognition!! He just assumed a symmetric time invariance to his mentor Louis de Broglie's Law of Phase Harmony. Actually de Broglie's Law of Phase Harmony is noncommutative as Professor John G. Williamson points out. thanks. See The Quicycle channel for details.

0 seconds ago
Kurt Godel said Time Travel is possible if there are no personal desires. This is true and how precognition works via meditation. I know this from experience. Read the book "Transcendent Dreaming" by Christina Donnell for details - Ph.D. in psychology and shamanic meditation Tai Chi practitioner.

1 second ago
Ed Fouche's Alien Rapture book repeats the same false narrative from the Stargate Conspiracy expose of Lynn Picknett and Clive Prince so makes sense Walter's dad picked up the same false narrative about underground aliens or whatever - Demos or whatever. Fouche's superconducting mercury MHD propulsion gravity cancelling is totally corroborated by googlescholar! The ET alien backstory? Military disinfo a la Greg Bishop, Mark Pilkington, Nick Redfern, William Lyne, etc.