filmov
tv
How to complete the square (when solving quadratic equations)
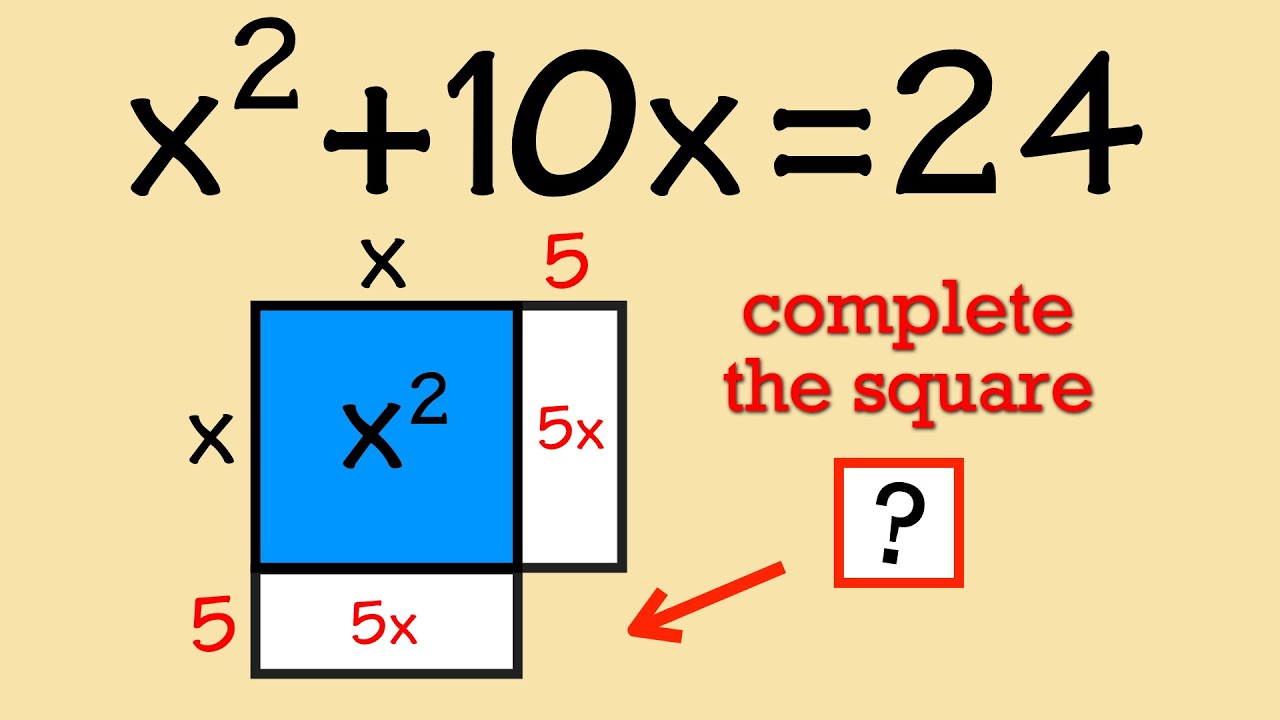
Показать описание
Let's discuss completing the square method when we are solving quadratic equations! We learn how to solve quadratic equations in 9th grade algebra but when we cannot solve a quadratic equation by factoring, we will have to use either completing the square or the quadratic formula. In fact, there's a geometric meaning behind the term completing the "square".
-----------------------------
-----------------------------
#math #algebra #mathbasics
-----------------------------
-----------------------------
#math #algebra #mathbasics
Solving Quadratic Equations By Completing The Square
Solve by completing the square | Step by Step Technique
The FASTEST Way To Complete The Square!! (in 48 seconds)
Solve by Completing the Square: Step-by-Step Technique
GCSE Maths - How to Factorise Quadratics by Completing the Square (Part 1 - Factorise When a=1) #52
Completing The Square Method | Quadratic Equation | asH maths
How to Solve By Completing the Square (NancyPi)
Solving a quadratic by completing the square
Integration Techniques Part 1e #maths #mathematics #education
Complete the square!
Complete the square - FAST and EASY!
Solve quadratic equation by Completing square method
Completing the Square Visually
Complete Square Grade 11
Solving a quadratic by completing the square
Completing The Square Explained In 1 Minute!
Completing the Square when a is Greater than One | GCSE Maths 2025
Beautiful Visual Explanation of Completing the Square
Completing the Square (visual proof)
Complete the Square
How To Solve Quadratic Equations By Completing The Square
Completing the Square 2 - Corbettmaths
Completing the Square
How to Solve Quadratic Equations by Completing the Square? Grade 9 Math
Комментарии
 0:07:57
0:07:57
 0:05:20
0:05:20
 0:00:49
0:00:49
 0:07:40
0:07:40
 0:05:14
0:05:14
 0:00:49
0:00:49
 0:17:33
0:17:33
 0:10:43
0:10:43
 0:00:51
0:00:51
 0:00:29
0:00:29
 0:04:48
0:04:48
 0:00:59
0:00:59
 0:00:54
0:00:54
 0:03:35
0:03:35
 0:04:10
0:04:10
 0:00:51
0:00:51
 0:00:58
0:00:58
 0:03:34
0:03:34
 0:01:26
0:01:26
 0:00:53
0:00:53
 0:13:07
0:13:07
 0:09:17
0:09:17
 0:05:36
0:05:36
 0:06:32
0:06:32