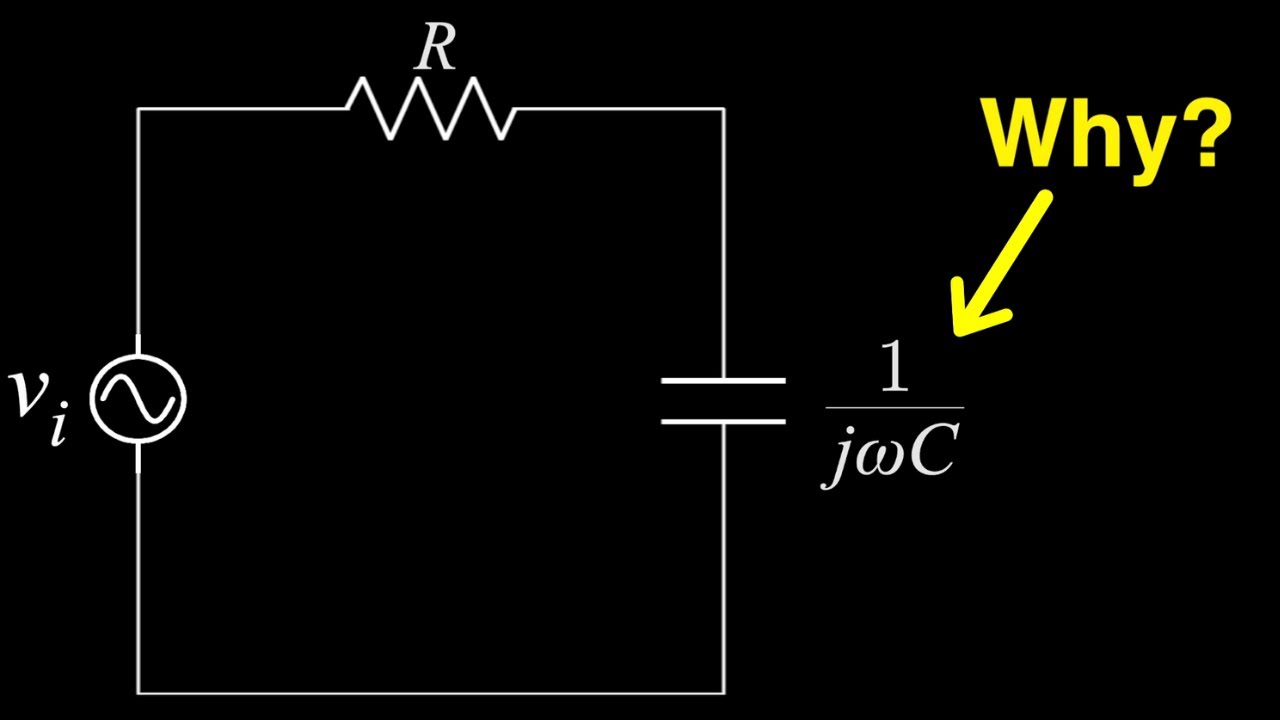
Why do Electrical Engineers use imaginary numbers in circuit analysis?

►Follow me

Join this channel to get access to perks:

►My Setup:

[myggmastaren]

short answer: because by using imaginary numbers we don't have to solve horrifying differential equations for every single circuit

[nestorv]

I'm a mathematician/physicist doing a career switch over to electrical engineering, and this has been the clearest introduction to Impedance I've seen. Thanks a lot

[rjScubaSki]

I remember having a 15 minute “discussion” with my professor in my EE lesson at uni (consistently in the top 5 in the world!) where he literally claimed there were an imaginary number of electrons moving around in the circuit. After a while people really can lose sight of their abstractions.

[iboyyobi]

This was mind blowing, this puts to rest my age old quest on how Laplace's transform converts differential into algebraic equations and the inverse Laplace does the opposite. Also had a smile on my face when I saw how Vc in an RC circuit literally maps to the total impedance of the circuit, just as in two resistors. I learned all of these 2 decades ago and it all came back to me. You don't need to do rote learning if you understand it deep at this level. A million thanks for all your efforts. Don't underestimate the value of your work, it brings a lot of smiles to a lot of people.

[marceloescalantemarrugo]

The math trick of changing from sinusoids to complex numbers is based on ignoring the transient part e^kt in the total response, but in general it take few miliseconds and can be ignored, so the trick is useful.

[jakoblenke]

I chose electrical engineering because of you, and I love it! This is literally what I‘m learning right now!

[legoyoda]

The part with the double angle formulas completely blew my mind! I really liked this video and sometimes wish you'd upload more of these!

[highcap]

Because real numbers are too easy for us!

[me]

In electrochemistry, phasor notation becomes really useful when investigating the electrode-electrolyte interface, in a technique called electrochemical impedance spectroscopy (EIS). The resistor component is modelled by the real impedance of charge transfer (Zct) and the real impedance of solution (Zs), and the imaginary impedance modelled by the electrical double-layer's capacitance (Zdl). Zdl and Zct are in parallel, and that parallel system is in series with Zs. It's a fairly simple circuit, but as you sweep the frequency, you can get a really nice pair of plots to model at which frequencies you have maximum and minimum impedance within a range.

The plot of combined impedance with respect to frequency is called the Bode plot, which shows the big picture of impedance. Then for each point of data given, you can break the combined impedance into real and imaginary components and get what is called the Nyquist plot, which is probably one of my favorite things in the world. I love it so much because Nyquist plots give you a really nice dome-like curve, the peak of which tells you the maximum capacitance of the EDL, the farthest right point of which tells the maximum impedance of charge transfer, and beyond that, you can see if charge transfer becomes less influential than mass transfer below a certain frequency.

I hope you'll do a deep dive into EIS at some point. It's just so cool. Also really useful for engineering things related to energy conversion and storage, which is something I'm sure a lot of your subscribers (me included) are very passionate about.

[karlkawano]

I wish you were my professor in the early 90's when I did my EE. I remember I had a lot of confusion at first and it took a lot of hours of studying to finally get it. Your explanation is so clear it's amazing! Thank you!

[anirbane_]

Going to Graduate as an Electrical Engineer in June, 2024. This video sparked inside me the excitement that I felt when I first learnt about these. 😄

[mostinho]

Right off the bat this video clarified what “phase” meant at 0:40. I knew it was related to the phase of the signal (how much it’s shifted back or forth) but I didn’t realize that it was the phase of the current in relation to the voltage, and that the derivative in the capacitor equation is what introduces it into the circuit. I graduated from ece 5 years ago, learned AC circuit analysis 8 years ago. We just learned to calculate things, not get an intuition for why things work. This video is delightful for someone who spent time calculating and wants to get some insight into how things work.

[Samir_Zouaoui]

Short answer : Fourier and Laplace Transform. Avoiding solving PDEs and ODEs to study system characteristics such as stability, equilibrium points, system delays and response to different signals with different frequencies.

[dorshreal]

As a current electrical enginggering student, this was a very informative video on a topic I had issues understanding before in class, this clears up the confusion.

[swamihuman]

- Excellent.
- Very well done: clear/concise/insightful.
- Thx.
- And, as a formally degreed engineer (Electrical), plus a self-taught math teacher, I especially appreciated your presentation.
- Keep up the great content...

[berralemramzi]

You cannot imagine how helpful this video is for me, Everyone in my class doesn't seem to care why we are suddenly using complexe numbers on vibrations and electricity, Thank you so much !

[Kira-vsnp]

i LOVE your vids, they're so helpful . would love to see you make vids on the Math in Machine Learning!

[moukafaslouka]

Or you can use a Laplace Transform to convert a differential equation into its algebraic equivalent. Solve. Then use Inverse Laplace Transform. This way, you are not restricted to just sinusoidal inputs.

[fifaham]

That was very nice refresher. Thank you.

[Zeitaluq]

Top lesson. Well done and plenty to expand on as individual work through to check the solutions.