filmov
tv
Proof That Zero Does Not Exist

Показать описание
In this video I will show that zero does not exist. This video actually shows a really key concept that comes up in calculus/advanced calculus. Please leave any comments in the comment section below.
If you enjoyed this video please consider liking, sharing, and subscribing.
There are several ways that you can help support my channel:)
************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course
Advanced Calculus Course
Calculus 1 Course
Calculus 2 Course
Calculus 3 Course
Calculus Integration Insanity
Differential Equations Course
College Algebra Course
How to Write Proofs with Sets Course
How to Write Proofs with Functions Course
Statistics with StatCrunch Course
Math Graduate Programs, Applying, Advice, Motivation
Daily Devotionals for Motivation with The Math Sorcerer
Thank you:)
#math #proof #zero
If you enjoyed this video please consider liking, sharing, and subscribing.
There are several ways that you can help support my channel:)
************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course
Advanced Calculus Course
Calculus 1 Course
Calculus 2 Course
Calculus 3 Course
Calculus Integration Insanity
Differential Equations Course
College Algebra Course
How to Write Proofs with Sets Course
How to Write Proofs with Functions Course
Statistics with StatCrunch Course
Math Graduate Programs, Applying, Advice, Motivation
Daily Devotionals for Motivation with The Math Sorcerer
Thank you:)
#math #proof #zero
Proof That Zero Does Not Exist
Why can't you divide by zero? - TED-Ed
Is zero a number? Does it exist? Does anything?? #shorts
Why does 'x to the zero power' equal 1?
Problems with Zero - Numberphile
Dividing by zero?
Prove that Zero Factorial is Equal to One
Is Zero Even? - Numberphile
The Man Who Invented Zero
Why “probability of 0” does not mean “impossible” | Probabilities of probabilities, part 2
Zero Factorial - Numberphile
Is zero a natural number?
I Learned How to Divide by Zero (Don't Tell Your Teacher)
What Happens to the Body in Zero Gravity?
1 divided by 0 is equal to || One by zero | Division by Zero
Zero Knowledge Proofs - Computerphile
Absolute Zero: Absolute Awesome
Prove the Limit of conjugate(z)/z as z approaches zero Does Not Exist Complex Analysis
How to Stop Zero when Copying Blank Cells in Excel
Zero Knowledge Proof (with Avi Wigderson) - Numberphile
Zero Knowledge Proofs
How Zero Build Could Ruin Fortnite...
Invention Of Zero - The Dr. Binocs Show | Best Learning Videos For Kids | Peekaboo Kidz
Harry Potter Makes Zero Sense
Комментарии
 0:09:20
0:09:20
 0:04:51
0:04:51
 0:01:00
0:01:00
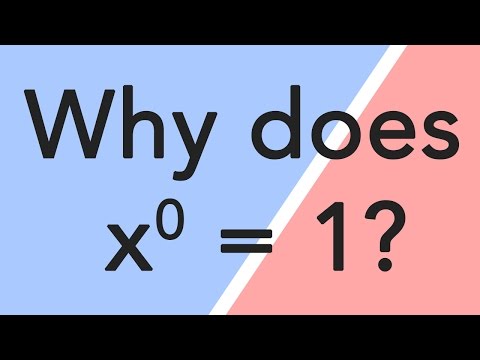 0:02:15
0:02:15
 0:13:00
0:13:00
 0:09:09
0:09:09
 0:01:58
0:01:58
 0:06:44
0:06:44
 0:00:58
0:00:58
 0:10:01
0:10:01
 0:07:36
0:07:36
 0:03:45
0:03:45
 0:07:36
0:07:36
 0:00:32
0:00:32
 0:00:49
0:00:49
 0:09:39
0:09:39
 0:03:16
0:03:16
 0:03:19
0:03:19
 0:00:44
0:00:44
 0:33:38
0:33:38
 0:10:16
0:10:16
 0:00:30
0:00:30
 0:07:17
0:07:17
 0:01:00
0:01:00