filmov
tv
Is zero a natural number?

Показать описание
Some argue that 0 is a natural number; others say it isn’t. Who is right?
Is zero a natural number?
Is zero a natural number?
Proof that Zero is a Natural Number
Why zero is in Whole number not in natural number ? #wholenumbers #numbersystem #numbers #natural
Is Zero a Natural Number?
Is Zero a Natural number?
Is zero a number? Does it exist? Does anything?? #shorts
What are Natural Numbers?
Proof of the Sum of Cubic Natural Numbers Formula
The Story of (almost) All Numbers
Why do numbers to the power of 0 equal 1?
Zero is a Number (Peano Postulate 1)
ASTOUNDING: 1 + 2 + 3 + 4 + 5 + ... = -1/12
Whole Numbers? Natural Numbers? Integers? 🤔 | Fun Math | Don't Memorise
Why can't you divide by zero? - TED-Ed
What are Natural Numbers? Number System
Is Zero an Even Number? | One Minute Bites | Don't Memorise
Classification of Numbers (Natural, Whole, Integers, Rational, Irrational, Real) - Nerdstudy
What are the Types of Numbers? Real vs. Imaginary, Rational vs. Irrational
Invention Of Zero - The Dr. Binocs Show | Best Learning Videos For Kids | Peekaboo Kidz
Number System ( Natural Number, Whole Number, Integer, Rational Number, Irrational Number, Real)
Check Weather 6 Raised Power 'n' Can End With The Digits Zero #shorts #puzzle
But WHY Exactly is Negative times Negative Positive?! [ Zero x Something is Zero ]
Facts about Zero | Zero & Its Facts | Properties of Zero | Mathematics | Study Tips | What is Ze...
Комментарии
 0:03:45
0:03:45
 0:01:30
0:01:30
 0:05:30
0:05:30
 0:01:01
0:01:01
 0:03:42
0:03:42
 0:04:04
0:04:04
 0:01:00
0:01:00
 0:01:34
0:01:34
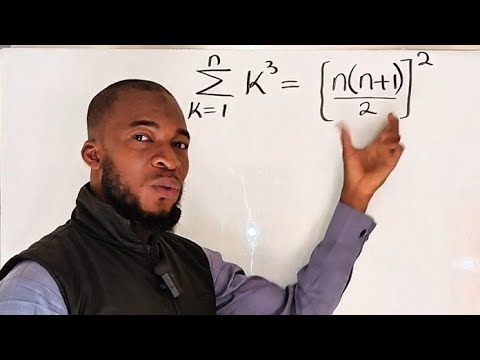 0:00:00
0:00:00
 0:11:32
0:11:32
 0:05:58
0:05:58
 0:04:46
0:04:46
 0:07:50
0:07:50
 0:00:34
0:00:34
 0:04:51
0:04:51
 0:04:20
0:04:20
 0:00:51
0:00:51
 0:07:58
0:07:58
 0:09:00
0:09:00
 0:07:17
0:07:17
 0:00:16
0:00:16
 0:00:19
0:00:19
 0:07:35
0:07:35
 0:01:00
0:01:00