filmov
tv
Introductory Real Analysis, Lec 3: Irrational Numbers, Supremums, Completeness, Sqrt(2) Exists
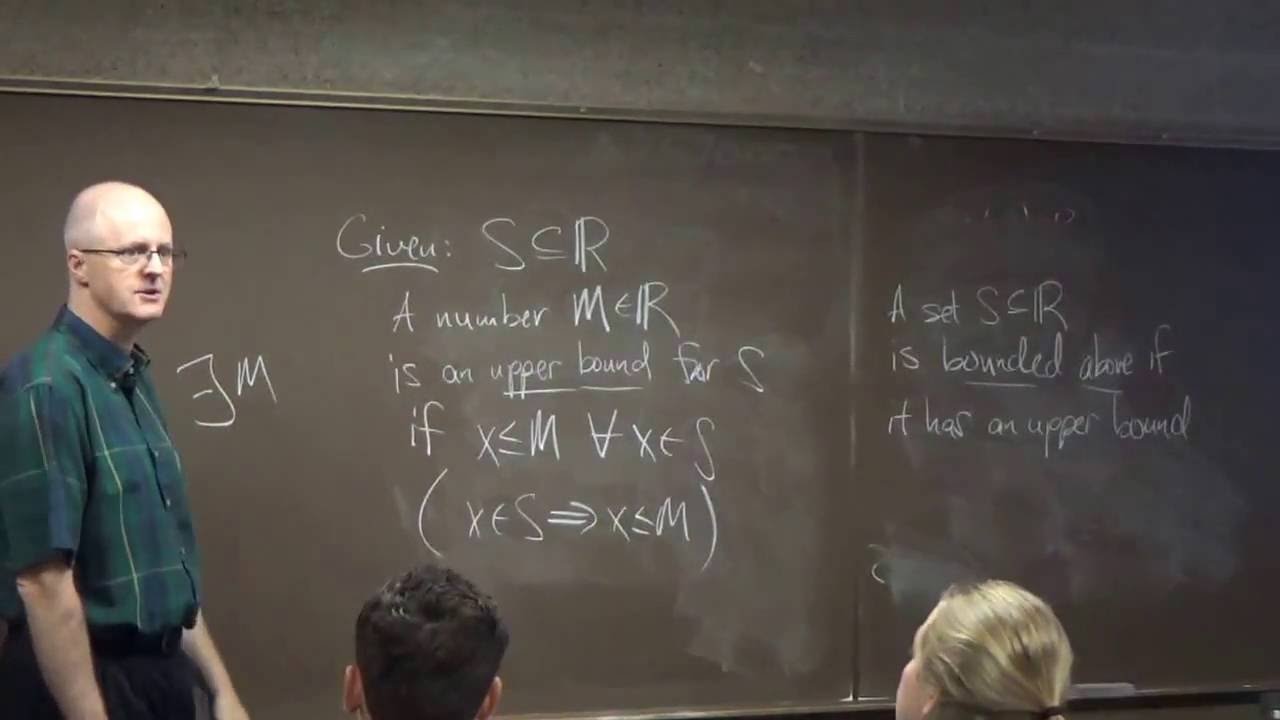
Показать описание
Bill Kinney, Bethel University Department of Mathematics and Computer Science. St. Paul, MN.
(0:00) 0.9999... = 1 is true.
(6:25) sqrt(3) is irrational.
(8:01) sqrt(6) is irrational.
(10:33) sqrt(2) + sqrt(3) is irrational.
(12:55) Statement of the completeness axiom.
(14:31) Definition of what it means for a number to be an upper bound of a set of real numbers.
(17:48) Definition for a set to be bounded above.
(19:46) Examples.
(20:42) Definition of the supremum of a set of real numbers.
(22:55) Examples of sups.
(27:54) Visual description of the proof that every nonempty set of real numbers that is bounded below has an inf.
(30:19) Scratch work details of how to think about the proof that sqrt(2) exists using the completeness axiom.
(49:09) Definition of what it means for a set to be dense in the set of real numbers R.
(51:32) The set of rational numbers Q is dense in the set of real numbers R.
AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.
Introductory Real Analysis, Lec 3: Irrational Numbers, Supremums, Completeness, Sqrt(2) Exists
Gilbert Strang: Linear Algebra vs Calculus
Intro Real Analysis, Lec 19, Part 3: Review for Real Analysis Exam 2
Intro to Real Analysis, Lec 4: Cardinality, Cantor, Continuum Hypothesis, Ping Pong Ball Conundrum
Intro Real Analysis, Lec 17: Mean Value Theorem Corollaries, Definition of Riemann Integral
Intro Real Analysis, Lec 16, Part 1: Mean Value Theorem: Statement, Basic Examples, and Proof
Intro Real Analysis, Lec 37, Part 1: Taylor Series, Cantor Sets & Logistic Map, Review Topology
Intro Complex Analysis, Lec 3, Polar Form, Principal Value of Arg, Basic Mappings
Intro Real Analysis, Lec 21: Convergence of Riemann Sums, Fundamental Theorem of Calculus
Intro Real Analysis, Lec 15: Uniform Continuity, Monotone Functions, Devil's Staircase, Derivat...
Intro Real Analysis, Lec 37, Part 2: Review Topology, Quick Review of Other Real Analysis Topics
Real Analysis I (lec. 0.3.B). Induction & Recursion.
Intro Real Analysis, Lec 22: Review Properties of Integrals and Fundamental Theorem of Calculus
Intro Real Analysis, Lec 5: Archimedean Property of R, Cantor's Theorem, Sequences, Crazy Funct...
Real Analysis I (lec. 3.1.E) Continuity of a Function at a Point
Intro Real Analysis, Lec 29: The Most Beautiful Equation in the World, Taylor Series Calculations
Intro Real Analysis, Lec 11: Continuity and the Intermediate Value Theorem (climbing Monk Story)
Intro Real Analysis, Lec 19, Part 1: Conditions for Riemann Integrability
Razavi Electronics 1, Lec 3. Diffusion, Intro. to PN Junction
Intro Real Analysis, Lec 32: Open and Closed Sets in the Real Line and in the Plane
Intro Real Analysis, Lec 19, Part 2: Riemann Integrability, Linearity of Integral, Review for Exam 2
Intro Real Analysis, (Rest of) Lec 14: Variation of a Function, Derivative Calculation Using Limits
Intro Real Analysis, (Most of) Lec 14: Uniform Continuity Non-Examples, Variation of a Function
Real Analysis I (lec. 3.3.H) Uniform Continuity : Open, Closed, Compact Sets
Комментарии
 0:52:54
0:52:54
 0:02:14
0:02:14
 0:10:34
0:10:34
 0:57:48
0:57:48
 0:56:27
0:56:27
 0:33:53
0:33:53
 0:21:54
0:21:54
 0:58:17
0:58:17
 0:56:16
0:56:16
 0:54:44
0:54:44
 0:34:24
0:34:24
 0:15:10
0:15:10
 0:54:54
0:54:54
 0:55:02
0:55:02
 0:17:35
0:17:35
 0:55:40
0:55:40
 0:56:28
0:56:28
 0:23:59
0:23:59
 1:08:59
1:08:59
 0:56:16
0:56:16
 0:23:59
0:23:59
 0:10:05
0:10:05
 0:43:37
0:43:37
 0:12:24
0:12:24