filmov
tv
Intro Real Analysis, Lec 29: The Most Beautiful Equation in the World, Taylor Series Calculations
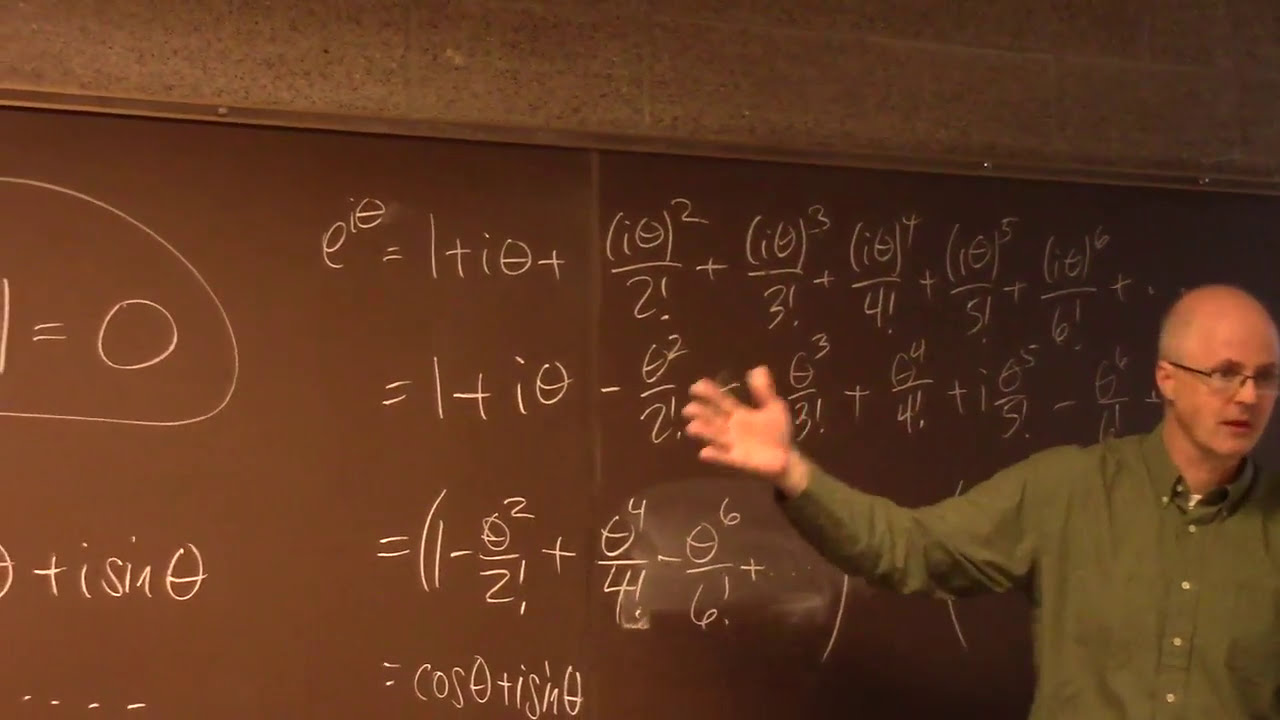
Показать описание
Introduction to Real Analysis, Lecture 29.
(0:00) Start
(0:27) What is the most beautiful equation in the universe? It is e^(i*pi)+1=0. It has the five most important numbers, the three most important operations, and the most important equivalence relation in one simple statement.
(2:31) Why is it true? Because of Euler's identity, which can be derived using the Taylor series for e^x, sin(x), and cos(x). It is assumed that the series can be combined by rearrangement (it can be done because they are absolutely convergent series).
(9:33) Visualize Euler's identity in the complex plane with Mathematica (and in terms of the Taylor expansion of e^(x)).
(17:20) We will continue focusing on calculations today. The Taylor series for e^(x) as a summation (with sigma notation). Confirm that it converges for all x with the Ratio Test (so the interval of convergence is from -infinity to infinity and the radius of convergence is infinity).
(22:53) Taylor series for cosine and sine in summation form.
(25:39) Find the Taylor series for x^2*sin(x^3) by substitution and multiplication. Check by using the Mathematica function Series.
(30:01) Know the Taylor series for 1/(1-x) (based on the geometric series formula) and be able to find Taylor series for related functions by substitution (such as for 1/(1+x) and 1/(1+x^2)). The interval of convergence in each of these cases is the open interval (-1,1).
(33:41) Integrate 1/(1+x) term by term to get the series for ln(1+x). This happens to converge on the half open half closed interval (-1,1] (when x = 1 the series converges conditionally (non-absolutely) to ln(2), but the convergence is slow).
(38:54) The convergence will be uniform on any proper closed subinterval.
(39:44) Integrating the Taylor series for 1/(1+x^2) term by term gives the series for the arctangent function arctan(x) = tan^(-1)(x). This also allows us to get an infinite series expansion for pi (with a slowly converging alternating series).
(42:35) Differentiate the Taylor series for 1/(1-x) = (1-x)^(-1) to find the Taylor series for 1/(1-x)^2 = (1/(1-x))^2. This can also be confirmed by multiplication of Taylor series.
(46:45) Use algebraic tricks to find the Taylor series for 5/(7+3x) centered at x = 6. Check it with the Mathematica function Series. The interval of convergence is for those values of x within 25/3 of the number 6.
(52:11) Comments about two homework problems 1) related to pointwise convergence of the sum of two pointwise converging sequences of functions and 2) related to showing that absolute convergence implies convergence.
AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.
Комментарии
 0:55:40
0:55:40
 1:09:38
1:09:38
 0:49:45
0:49:45
 0:55:42
0:55:42
 0:10:05
0:10:05
 0:33:53
0:33:53
 0:40:54
0:40:54
 0:41:58
0:41:58
 1:58:32
1:58:32
 0:00:14
0:00:14
 1:19:57
1:19:57
 0:43:37
0:43:37
 0:21:10
0:21:10
 0:52:34
0:52:34
 0:09:59
0:09:59
 1:12:18
1:12:18
 0:00:48
0:00:48
 0:12:47
0:12:47
 0:34:24
0:34:24
 0:08:42
0:08:42
 0:22:29
0:22:29
 0:54:38
0:54:38
 0:50:57
0:50:57
 0:40:57
0:40:57