filmov
tv
Math for fun#1, design your limit
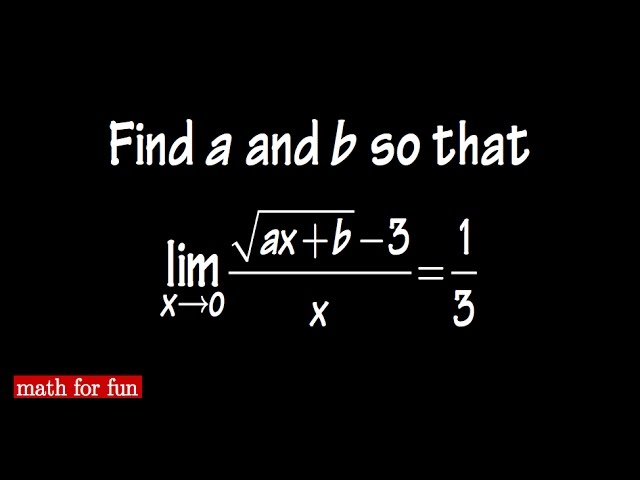
Показать описание
Calculus 1 limit.
Math For Fun#1, Limit
math for fun series#1, limits, precalc, calculus, algebra.
Math For Fun#1, Limit
math for fun series#1, limits, precalc, calculus, algebra.
Math for fun#1, design your limit
Easy Book Cover Design | Math #shorts #nhuandaocalligraphy #diy #bookcover #satisfying
Memorization Trick for Graphing Functions Part 1 | Algebra Math Hack #shorts #math #school
Math for fun, 1, 2, 3, 4, 5, 8, ____, ____, calculus 2 'find the pattern' for the sequence
Grant Sanderson (3Blue1Brown): Best Way to Learn Math | AI Podcast Clips
Math for fun#12, inf p-series over alternating inf p-series
Math for fun, find the value using calculus!
If you are a genius solve this! Math Game Challenge!!!
Human Calculator Solves World’s Longest Math Problem #shorts
HOW CHINESE STUDENTS SO FAST IN SOLVING MATH OVER AMERICAN STUDENTS
How To Self-Study Math
Anyone Can Be a Math Person Once They Know the Best Learning Techniques | Po-Shen Loh | Big Think
Easy Math Front Page Design for School ✏️ #shorts #frontpage #nhuandao
Front Page idea: Math ✨ #frontpage #nhuandaofrontpage #subjects #shorts
The 7 Levels of Math
BUZZ!!! Fun Math Game for the Classroom
5 DIY Games to Practice Addition | Fun Math for Children
9 TIMES TABLE #shorts #math #maths #mathematics
🏡 Have Fun Practicing Math at Home!
Multiplication Flowers!! Math for Kids! EASY Math! #mathforkids #multiplication #timestabletrick
This Video Will Make You Better At Math
Stop Trying to Understand Math, Do THIS Instead
The Beauty of Math - Zimmer [Motivational]
This Math Video so Cursed, it'll make your Dad Buy Milk
Комментарии
 0:05:42
0:05:42
 0:00:26
0:00:26
 0:00:15
0:00:15
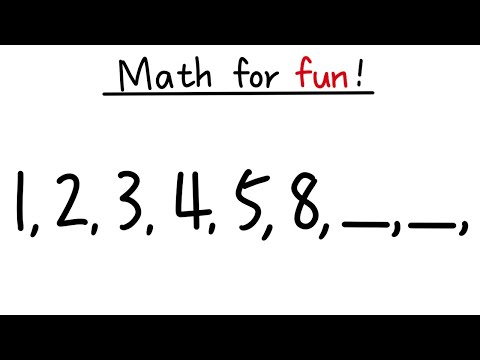 0:04:50
0:04:50
 0:03:22
0:03:22
 0:09:13
0:09:13
 0:07:05
0:07:05
 0:00:28
0:00:28
 0:00:34
0:00:34
 0:00:23
0:00:23
 0:08:16
0:08:16
 0:03:53
0:03:53
 0:00:49
0:00:49
 0:00:34
0:00:34
 0:08:44
0:08:44
 0:04:30
0:04:30
 0:06:11
0:06:11
 0:00:23
0:00:23
 0:00:16
0:00:16
 0:00:44
0:00:44
 0:04:52
0:04:52
 0:05:21
0:05:21
 0:06:38
0:06:38
 0:00:48
0:00:48