filmov
tv
Math for fun, find the value using calculus!

Показать описание
Math for fun, Series of n/3^n = ?
Value of the sum of n/3^n, from n = 1 to inf.
Value of the sum of n/3^n, from n = 1 to inf.
Math for fun, find the value using calculus!
Math for fun#1, design your limit
Math for fun, how many rectangles?
How Do You Make Math Fun
Learning Math
Fun Math Warmup Problem
The 7 Levels of Math
Norway Math Olympiad Question | You should be able to solve this!
Triangles Perimeter and Area #math #matematicas #geometry #stem #learntocode
Math for fun, 1, 2, 3, 4, 5, 8, ____, ____, calculus 2 'find the pattern' for the sequence
Math for fun#15, GEOMETRIC SERIES WANNABE?
Math for fun#12, inf p-series over alternating inf p-series
If you are a genius solve this! Math Game Challenge!!!
I make math fun | Khalil Fuller | TEDxUnisinos
Five Principles of Extraordinary Math Teaching | Dan Finkel | TEDxRainier
Fast Multiplication Trick | Interesting math tricks #maths #shorts
Stop Trying to Understand Math, Do THIS Instead
9 Math Riddles That'll Stump Even Your Smartest Friends
Math & Movement
The Hardest Math Test
Human Calculator Solves World’s Longest Math Problem #shorts
Math game |Paper Game |Home made game #math #mathgames #papergames #shorts #viral #viralshort #short
Math for fun#3, highest & lowest points on a tilted ellipse?
How to find the Mean, Median, Mode and Standard Deviation. EmSAT Math!
Комментарии
 0:07:05
0:07:05
 0:05:42
0:05:42
 0:13:54
0:13:54
 0:03:09
0:03:09
 0:02:37
0:02:37
 0:02:53
0:02:53
 0:08:44
0:08:44
 0:03:21
0:03:21
 0:00:43
0:00:43
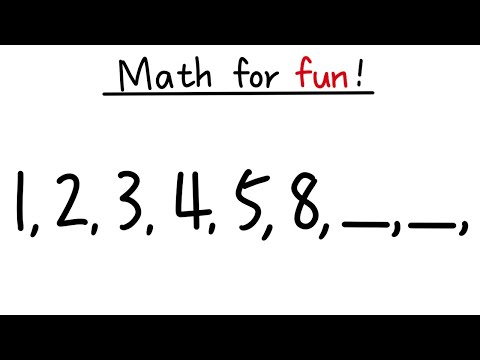 0:04:50
0:04:50
 0:14:05
0:14:05
 0:09:13
0:09:13
 0:00:28
0:00:28
 0:11:51
0:11:51
 0:14:42
0:14:42
 0:00:28
0:00:28
 0:05:21
0:05:21
 0:06:40
0:06:40
 0:03:06
0:03:06
 0:00:28
0:00:28
 0:00:34
0:00:34
 0:00:14
0:00:14
 0:08:39
0:08:39
 0:26:07
0:26:07