filmov
tv
Math for fun, 1, 2, 3, 4, 5, 8, ____, ____, calculus 2 'find the pattern' for the sequence

Показать описание
Math for fun, 1, 2, 3, 4, 5, 8, ____, ____,
----------------------------------------
#blackpenredpen #math #calculus #apcalculus
----------------------------------------
#blackpenredpen #math #calculus #apcalculus
Animation vs. Math
math for fun, -1=1? (with Euler's formula)
Learning Math
Learn Addition up to 10 | Addition 1 to 9 | Math for Kindergarten & 1st Grade | Kids Academy
Math for fun, 1, 2, 3, 4, 5, 8, ____, ____, calculus 2 'find the pattern' for the sequence
Wendy Alex and Lyndon Learn Math & Numbers for the School Exam | Fun Kids Videos
If you are a genius solve this! Math Game Challenge!!!
Meet the Math Facts - Addition & Subtraction Level 1 (FREE) | Preschool Prep Company
Math for fun, sin(sin(z))=1
BUZZ!!! Fun Math Game for the Classroom
Math Quiz for Kids | One Digit Addition Quiz | Mental Math Quiz for Kids | Quiz Time
This simple game makes kids better at math
'Math Whiz!' Addition Song /// Danny Go! Kids Learning Songs for Kindergarten
The Simplest Math Problem No One Can Solve - Collatz Conjecture
Meet the Math Facts - Addition & Subtraction Level 2 (FREE) | Preschool Prep Company
Adding & Subtracting! | Mini Math Movies | Scratch Garden
Math & Movement
Fractions! | Mini Math Movies | Scratch Garden
Math for fun#1, design your limit
The 7 Levels of Math
Emma and Andrew Learn Shapes and Math with Fun Kids Toys | Educational Videos for Children
Math for fun#11, 1+1/2+1/3+1/4+1/6+1/8+1/9+1/12+...=?
MATH SONG - I LOVE MATH
Meet the Math Facts - Multiplication & Division Level 1 (FREE) | Preschool Prep Company
Комментарии
 0:14:03
0:14:03
 0:02:51
0:02:51
 0:02:37
0:02:37
 0:02:18
0:02:18
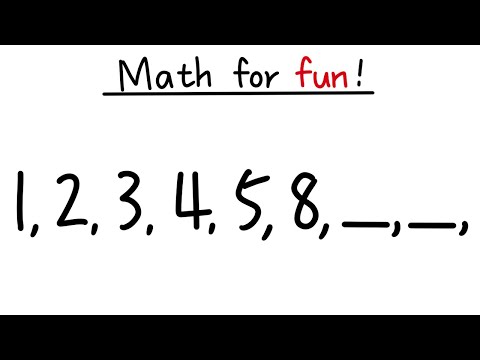 0:04:50
0:04:50
 0:15:05
0:15:05
 0:00:28
0:00:28
 0:59:22
0:59:22
 0:11:13
0:11:13
 0:04:30
0:04:30
 0:16:06
0:16:06
 0:02:07
0:02:07
 0:03:45
0:03:45
 0:22:09
0:22:09
 1:03:26
1:03:26
 0:07:27
0:07:27
 0:03:06
0:03:06
 0:06:42
0:06:42
 0:05:42
0:05:42
 0:08:44
0:08:44
 0:14:08
0:14:08
 0:08:17
0:08:17
 0:01:26
0:01:26
 1:33:20
1:33:20